- ...
Korrekturen1
- Namen der Studenten, die
Korrekturen geliefert haben: Stefan
Freudenberg, Svend-Age Biehs
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gehalten2
- mit wechselnder Resonanz: einmal stieg die Zahl der Hörer stetig über
beide Semester hinweg bis zum Ende, einmal stieg das Durchschnittsalter auf über
70 Jahre,
- dem Alter meines letzten aber hoch aufnahmefähigen
und interessierten
Hörers..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Vorlesung3
- ein erster Versuch einer solchen
propädeutischen Veranstaltung wurde durch G. Süßmann
(mit seinem Assistenten E.R.H.) an der Universität Frankfurt
durchgeführt (1995).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
angefragt4
- siehe Abschnitt
'Transcripts'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Orten5
- unvergessen ist mir die heftige
Diskussion mit Mitstudenten anderer Fächer auf einem
Segeltörn auf der Elbe zu der
Frage, ob und wann eine Flasche auf einer Waage schwerer oder leichter gemessen wird,
wenn in ihr eine Fliege sitzt, fliegt, sich setzt, -jeweils zu diskutieren für die
Fälle, wenn der Korken auf der Flasche sitzt oder daneben gelegt wird...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gelehrt6
-
In der Bezeichung trennen wir das Bild (hier: H) von der Abbildung
(hier:
dtt als zweifacher Ableitung nach der Zeit), und dem Abbild
(hier: g), anstelle der redundanten und trotzdem unklaren und mißverständlichen
Bezeichnung dH(t)/dt .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Verwendung7
- Es gilt ja zu unterscheiden zwischen der Gleichheit zweier
bekannter Objekte (ein Kilo Birnen wiegen genausoviel wie
zwei Pfund Birnen), einer experimentell
zu prüfenden These (das vorliegende Kilo Äpfel wiegt genauso viel wie die
vorgelegten drei Birnen), ein Kilo seien zwei Pfund (hier wird das als unbekannt angenommene
Kilo durch das als bekannt angenommene Pfund eingeführt, diese 'Gleichheit'
hat also eine Richtung, oft wird daher (z.B. in Programmiersprachen) geschrieben
1Kilo:= 2Pfund.
Schließlich gibt es Entsprechungen, Analogien, Ähnlichkeiten, usf., die oft
ebenfalls einfach mit einem Gleichheitssymbol abgekürzt werden..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Pfade8
-
Der Leser möge dies ruhig für sehr wenige Bahnen auf einem groben
Zeit/Raumgitter und zum Beispiel eines freien Teilchens in Ruhe
oder konstanter Geschwindigkeit probieren. Es ist immer überraschend,
wie gut es funktioniert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
erspart.9
- Die korrekte Mechanik ist ein Standardgebiet
der Theoretischen Physik, die Lehrbücher findet man unter Titeln wie
'Quantenmechanik'..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...910
- Der Leser möge dies selbst
versuchen: Man nehme eine kräftefreie Bewegung (V=0).
Dann teile man das Zeitintervall
0 < t < t1 in
drei gleiche Teile, ebenso die Ortsvariable 0 < h < Hin drei Teile und nehme nur Bahnen, die stets
zwischen irgendzwei Gitterpunkten geradlinig
vom Startpunkt zu einem Gitterpunkt der 'Zeitebene'
t=t1/3, zu irgendeinem der drei Gitterpunkt der Ebene t1=2t/3schließlich zum festen, weil ja beobachteten Zielpunkt fliegen.
Sodann berechne man die Vorschrift für die 33=27 möglichen
Bahnen und addiere die Ergebnisse. - Fantastisch, wie gut sich die
Newtonsche Mechanik ergibt..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...änden.
11
- Beispiel: ob ich mein Fahrrad ins Institut gebracht habe, oder ob
das Fahrrad mich ins Institut gebracht hat, ist physikalisch unerheblich).
Bitte testen Sie doch die Reaktion Ihrer (nichtphysikalisch vogebildeten)
Mitbürger mit solchen transitiven Aussagen, und fragen Sie dann nach einer
Möglichkeit, experimentell zwischen beiden Alternativen zu unterscheiden.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nicht..12
- Ein Kind schwingt ein Seil, das von außerhalb des Gartens
durch den Staketenzaun (senkrechte Balken eines Jägerzaunes)
zur Hauswand führt.
Wenn das Seil speziell in Richtung der Staketen schwingt, hat es keinen
Widerstand, es ändert den Zustand des Zaunes nicht, und der Zaun bewirkt
keine Änderung (Störung) des Schwingungszustandes des Seils.
Wäre es Nacht, könnte dann das Kind nicht feststellen,
ob überhaupt ein Zaun da ist...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Die13
- Wem die epische Breite
zuwider ist, der warte auf den mathematischen Anhang,
aber der Absprung zu aktuellen Forschungsgebieten der Physik
mit grundlegenden neuen Erkenntnissen über die RaumZeit
erfolgt aber gerade aus diesem Kapitel heraus, und der eilige
Leser übersieht das vielleicht; Nehmen wir als Beispiel die
Idealisierung des Fadens. Vorausgesetzt ist doch hier die
mechanische Realisierung mittels Materie. Dies bereitet jedoch
im subatomaren Reich Schwierigkeiten: Die Teilchen kleinster Raumausdehnung
sind die Elektronen, die also hervorragend geeignet sein sollten als
Material, den feinsten realisierbaren Faden zu spinnen.
'Leider' ist es bisher jedoch nicht gelungen, den Elektronen überhaupt
eine Raumausdehnung zuzusprechen, genauer: sie haben diese Eigenschaft
überhaupt nicht. Damit sind aber zugleich die Eigenschaft der
Homogenität und Isotropie des Raumes bei diesen sehr kleinen
Nachbarschaften prinzipiell nicht realisierbar (genügend weit unterhalb
10-15cm). Ergebnisse der aktuellen Forschung in der Theoretischen
Physik haben bereits eine Fülle von Forderungen an den Bereich der
Feinststruktur des Raumes gestellt und den Zusammenbruch der Homogenität
des Raumes für Abstände im Bereich der Planck-Länge (10-48cm)
vorausgesagt. Aber der Leser des ersten Semester muß sich eben gedulden,
noch ist ja nicht einmal eingeführt, was ein Abstand in der Physik
überhaupt ist..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Paralleltransport14
-
das hat natürlich garnichts zu tun mit einer Parallelen in der Euklidischen
Geometrie, sondern bedeutet 'längs von'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Stell15
- Das norddeutsche Wort
steht für eine definiierte Untermenge von
Objekten, z.B. mein Stell Seekarten für eine
Reise nach England.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 16
- in contrast Mathematics
is much 'simpler': there just any set of objects with any set of
rules is equally worthwhile to think about iff a given set of rules is
free of logical conflicts and if it appears intellectually of interest
to the only real object in this world of thoughts, the mathematician..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sind:17
- Dieser Text richtet sich an Anfangssemester der Physik, um sie
einzugewöhnen, Korrekturen und Bemerkungen werden gerne aufgenommen,
auf alle Feinheiten wurde jedoch bewußt verzichtet, erst recht auf
mathematische Beweise. Der hier vorgespannte Leser sei auf das exzellente
Buch von Thirring verwiesen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Columbus18
-
Cristopher Columbus entdeckte durch die intuitive Erfassung der Aussage dieses
Satzes Amerika: alle Punkte unserer Erde seien eine dreidimensionale
(es gibt mindestens drei unabhängige Kurven durch jeden Punkt des
Inneren, deren Nachbarschaft beidseitig zu ihr gehört.)
orientierte Punktmenge. Die Menge der Randpunkte (für die es zu
jedem Punkt nur
mindestens zwei unabhängige Kurven durch
jeden Randpunkt gibt), deren
Punkte dazu gehören.
Der Satz von Columbus bedeutet dann, daß die Erdoberfläche keinen
Rand haben KANN. Alle Randpunkte der dreidimensionalen Erde sind
bezüglich ihrer Nachbarschaftseigenschaften gleichartig.
Er machte sich, im Gegensatz zu damaligen Gelehrten KEINE Sorgen,
plötzlich bei der Suche nach Amerika über den Rand der Erdoberfläche
abzustürzen, -es kann und darf ihn nicht geben.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gebiete19
- Auf
die mit den höheren Semestern zu
pflegende Diskussion der Eigenschaften
des Limes
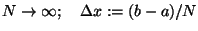 wird hier
ebensowenig behandelt wie die
Verallgemeinerung auf gekrümmte
Räume. Während dieser Limes
'abzählbar unendlich wird, ist gerade
einer der großen Fortschritte der
hier eingeführten Differentialformen,
daß sie überabzählbar
('reell') unendlich sind: für jeden
Punkt der Strecke [a,b] ist der
Integrand zu berechnen und alle diese
Ergebnisse aufzusummieren.
Der eigentliche Unterschied und
Fortschritt ist, daß bei Leibniz
die Differentiale
dxi zahlenwertig
sind und kommutieren, während sie als
elementare Differentialform
wird hier
ebensowenig behandelt wie die
Verallgemeinerung auf gekrümmte
Räume. Während dieser Limes
'abzählbar unendlich wird, ist gerade
einer der großen Fortschritte der
hier eingeführten Differentialformen,
daß sie überabzählbar
('reell') unendlich sind: für jeden
Punkt der Strecke [a,b] ist der
Integrand zu berechnen und alle diese
Ergebnisse aufzusummieren.
Der eigentliche Unterschied und
Fortschritt ist, daß bei Leibniz
die Differentiale
dxi zahlenwertig
sind und kommutieren, während sie als
elementare Differentialform
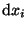 antikommutieren,
dxidxj=dxjdxi und so die
Orientierung der Integrationsgebiete
wiederspiegeln. Numerisch werden die
Integrale natürlich sowieso nur in
einer Gitternäherung (N endlich)
berechnet und dann haben die
Summanden dieser Verknüpfung
natürlich numerisch handhabbare
endliche Werte.
antikommutieren,
dxidxj=dxjdxi und so die
Orientierung der Integrationsgebiete
wiederspiegeln. Numerisch werden die
Integrale natürlich sowieso nur in
einer Gitternäherung (N endlich)
berechnet und dann haben die
Summanden dieser Verknüpfung
natürlich numerisch handhabbare
endliche Werte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Null20
- Als
Beispiel betrachten wir einen Würfel im
gewöhnlichen dreidimensionalen Raum.
Vielleicht sieht man ihm nicht an, daß die
Menge der Raumpunkte, die er ausfüllt, eine
orientierte Punktmannigfaltigkeit sind.
Zu ihm gehören zwei Sorten von Punkten: die
Punkte im Innern haben auf allen Kurven im R3,
die man durch sie legen kann, stets alle
Nachbarpunkte, sowohl vor wie hinter in=hm, im
Innern des Würfels. Durch die Randpunkte
lassen sich Kurven im R3 legen, bei denen der
eine Nachbarpunkt innen, der andere
außerhalb des Würfels liegen.
Diese Konstruktion zeigt die Orientierung der
Punktmenge, es gibt ein Innen und ein Aussen.
Die Menge
aller Randpunkte (die 'Haut' des
Würfels) nennen wir den Rand von ihm.
Diese Punktmenge hat zwei Diemnsionen und ist
ebenfalls orientiert.
Mit der gleichen Konstruktion, Kurven in die
durch einen Punkt dieser Randmenge gehen, und in
der zweidmensionalen Menge liegen, sieht man:
es gehören immer beide Nachbarpunkte einer
Kurve zur Menge, alle Punkte der Randmenge des
Würfels sind innere Punkte von ihr. Sie hat
also selbst als Rand nur die leere Menge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... kann.21
- Wieviel unabhängige Linien durch einen
Punkt der Grundmenge gibt es, auf denen man als Nachbarpunkte wieder Punkte aus
ihr findet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... genannt.22
- Man sieht, daß die Theorie der Integranden auch wesentlich
studienverkürzend ist..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....23
- In der frühen Entwicklung der Vektorrechnung führte man das
sogenannte Kreuzprodukt zweier Vektoren ein und bezeichnete dies als 'axialen
Vektor', der senkrecht zu den beiden Vektoren zeige.
Zwei Infinitesimale
dx1dx2 im
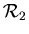 spannen eine
kleine Fläche auf, deren
Kreuzproduktvektor dann senkrecht dazu nach außen zeige,
die 'Flächennormale'. Ein echtes Kreuz, denn im
spannen eine
kleine Fläche auf, deren
Kreuzproduktvektor dann senkrecht dazu nach außen zeige,
die 'Flächennormale'. Ein echtes Kreuz, denn im
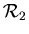 gibt es
keine dritte Richtung und sie wird weder mathematisch noch physikalisch,
um etwas auszurechnen,
an irgendeiner Stelle gebraucht.
d v hat nur Komponenten in Bezug
auf die Fläche und ihre inneren geometrischen Eigenschaften.
gibt es
keine dritte Richtung und sie wird weder mathematisch noch physikalisch,
um etwas auszurechnen,
an irgendeiner Stelle gebraucht.
d v hat nur Komponenten in Bezug
auf die Fläche und ihre inneren geometrischen Eigenschaften.
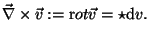 Nur der letzte Ausdruck ist für beliebig dimensionale Räume definiert und
die Komponenten haben ein eindeutiges
Koordinatentransformationsverhalten, das eines Tensors.
Nur der letzte Ausdruck ist für beliebig dimensionale Räume definiert und
die Komponenten haben ein eindeutiges
Koordinatentransformationsverhalten, das eines Tensors.
Der Leser möge sich ein Vergnügen daraus machen, die komplizierten
(englisch: clumsy) Notationen der Frühzeit umzurechnen:
Was ist
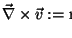 ?
In der Integrandenschreibweise kein Problem: mit der Merkregel
(ersetze ein Kreuzprodukt
?
In der Integrandenschreibweise kein Problem: mit der Merkregel
(ersetze ein Kreuzprodukt
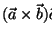 durch
durch
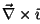 und das innere Produkt
und das innere Produkt
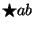 durch
durch
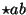 durch das äussere Produkt, so
erhalten wir
durch das äussere Produkt, so
erhalten wir
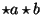 .
Einsetzen der Definitionen von der 1-Formen wie
.
Einsetzen der Definitionen von der 1-Formen wie
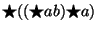 und Nutzen der Antisymmetrie
der Differentiale
dxidxj=-dxj�dxi ergibt als
schöne Übung die Null.
und Nutzen der Antisymmetrie
der Differentiale
dxidxj=-dxj�dxi ergibt als
schöne Übung die Null.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
analog.24
- Der Begriff in der Mathematik hat seine eigene
von der Umgangssprache andere Bedeutung gegenüber der Physik, weil
nur mit Gedankenkonstrukten gearbeitet wird. Dazu zwei stories:
''10 Eier sind zu kochen. Ein Hausmann nimmt einen Topf und kocht
die 10 Eier darin. Ein Mathematiker kocht im gleichen Topf ein Ei
und erklärt: 'die anderen Eier behandle ich analog'.
oder:
'Eine Gruppe von Ingenieuren und
eine Gruppe von Mathematikern fahren mit
dem Zug zu einer Tagung. Jeder Ingenieur besitzt eine Fahrkarte,
dagegen
hat die ganze Gruppe der Mathematiker nur eine einzige Karte.
Plötzlich ruft einer der Mathematiker: 'Der Schaffner kommt!',
worauf
sich alle Mathematiker in eine der Toiletten zwaengen. Der Schaffner
kontrolliert die Ingenieure, sieht, dass das WC besetzt ist und klopft an
die Tuer: 'Die Fahrkarte bitte!' Einer der Mathematiker schiebt die
:
Fahrkarte unter der Tuer durch und der Schaffner zieht zufrieden ab.
Auf der Rueckfahrt beschliessen die Ingenieure, denselben Trick anzuwenden
und kaufen nur eine Karte fuer die ganze Gruppe. Sie sind sehr verwundert,
als sie merken, dass die Mathematiker diesmal ueberhaupt keine Fahrkarte
haben.
Wieder ruft einer der Mathematiker:
'Der Schaffner kommt!'. Sofort
stuerzen die Ingenieure in das eine WC, die Mathematiker machen sich etwas
gemaechlicher auf den Weg zum anderen.
Bevor der letzte Mathematiker die Toilette betritt, klopft er bei den
Ingenieuren an: 'Die Fahrkarte bitte!'
Und die Moral von der Geschichte?
Ingenieure wenden die Methoden der Mathematiker an, ohne sie wirklich zu
verstehen.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Paare25
- Das ist dieselbe Zahl, wie
die Anzahl der Handschläge bei einer gegenseitigen Begrüßung von jedem mit
jedem auf
einer Party.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... desk26
- Available from the
Department of Physics, Carl von Ossietzky University, D-26111 Oldennburg.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... well.27
- Then you might prefer to use the .html version or
draw the .tex file and delete the many newpage commands.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...28
-
Of course we use the usual [cgs] system for dimensions:
a force has [g cm/s2], the electric field is defined by
K=qE and E=q/r2, thus we have the charge q[g1/2 cm3/2 s-1]
and the fieldstrength E[g1/2cm-1/2 s-1] .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gauß-law29
-
By acting on both sides the
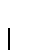 operator,
you gain
operator,
you gain
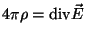 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
dimensions30
- :
a force has [g cm/s2], the electric field is defined by
K=qE and E=q/r2, thus we have the charge
q[g1/2
cm3/2s-1]
and the fieldstrength E[g1/2 cm-1/2 s-1],
no hassle with an
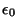 and new dimensions.
and new dimensions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.