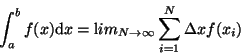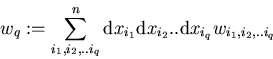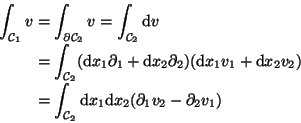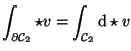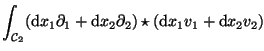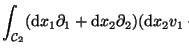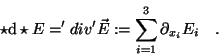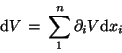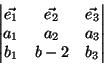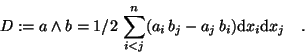17.1.2000: This conglomerat comprises fragments of two lines:
- a german language introduction to Physics for 1./2. term students,
- an english language introduction to mathematical physics for 1./2. term
students.
Leser, die sich anmelden (email an
den Autor
) werden informiert,
wenn ein Kapitel hinzugekommen ist,
sowie Antworten auf Lösungsvorschläge zu Übungsaufgaben erhalten.
Korrekturen und Hinweise sind bei einem Text in diesem frühen und
fragmentarischen Zustand besonders willkommen.
Hinweise auf Texte Dritter werden als link gerne aufgenommen.
Essays zum Thema
Einführung
in die Theoretische Physik
E.R.Hilf;
Fachbereich Physik, Carl von Ossietzky Universität Oldenburg.
begonnen: 15.10.1994; Reorganisation, Ergänzungen und
Korrekturen
1
5.1.2000
Materialien zur Ausbildung in den ersten beiden Semestern
Übungen:
Univ.Frankfurt, Prof. Roskilde.
Gegenwärtig (15.10.1999)
Wird mit dem BIS verhandelt, die Lizenz für das
Produkt des Harri Deutsch Verlages
CliXX Physik, cliXX Mathematik, Dektop Mathematik, Desktop Physik
zu erwerben.
Zum Schnuppern können Sie die Aufgaben im
Theoretikum und Projekte
an der U. Frankfurt (Prof. Stöcker) bearbeiten.
Ziel des Dokumentes ist:
-
den Arbeitsstilwechsel von der Schule zur Hochschule zu vollziehen, -
dies geschieht durch gemeinsames Üben,
-
Verständnis für theoretische Physik zu beginnen,
- dies geschieht durch gemeinsame Diskussion,
-
Einsicht in die Berufsqualifikationen/Anforderungen zu erhalten,
- dies geschieht durch Vergleichen und Unterscheiden
der verschiedenen Arbeitsstile und
Methoden zu den benachbarten Fächern.
Die entsprechende Vorlesung wurde mehrfach am Fachbereich Physik der Carl von Ossietzky Universität
Oldenburg gehalten2
Die Veranstaltung sollte aus einer
Vorlesung, einer Übung, einem Proseminar bestehen.
Dies war 1997 auch noch der Fall.
Die Vorlesung3
-
erste Einblicke in die Denkweise der Theoretischen
Physik,
-
wichtige erste Grunderfahrungen und Erkenntnisse, die sich in späteren
Veranstaltungen, - wenn das algebraische Rüstzeug vorausgesetzt werden kann,-
vertieft wiederfinden werden,
-
Beleuchtungen zu Rechnungen und mathematischen Formulierungen aus der Experimentalphysik,
- soweit gewünscht und
angefragt4. Experimentelle Zahlenwerte für
'Naturkonstanten' und deren Umrechnung, Maßeinheiten-Umrechnungen
pp. finden sich im
NIST (National Institute for Standards and Technology..
Übungen sollten integraler Bestandteil der Veranstaltung sein.
Viele Theoretiker sehen
Übungen, Seminare, Diskussionen als die zentralen Bestandteile des
Studiums, - und hier sind nicht nur Diskussionen unter den
Studenten oder mit dem Dozenten
gemeint, sondern mit jedem interessierten Menschen, -und sei es
am Familienküchentisch,
in der Bahn, im Lokal oder an anderen Orten5.
Das Proseminar ist der schüchterne Versuch, die angestrebte
Berufsqualifikation,
-die Fähigkeit, sich selbst einen Stoff anzueignen und darzustellen,
erstmals zu üben an selbstgewählten Beispielen.
Mögliche Themen wären:
-
Physikalische Begriffsbildungen und Hegels 'Physik'.
-
Das Pendel an der Scheunentür (und die eigene Erfahrung der Erdumdrehung).
-
Erhöhen sich die Sturmfluten bei Vertiefung der Ems -physikalische Modellierung und
die Tagespresseberichte.
-
Wie genau ist eigentlich numerisch die Bahn der Erde berechenbar?
-
Kausalität und Deterministik in der Physik.
-
Was haben (methodisch) große Entdeckungen und das Lösen einer Übungsaufgabe
in der Theoretischen Physik gemeinsam?
-
Kann man einen reißenden Tidenstrom hinaufschwimmen, und wie lange dauert das?
-
Wirbelstürme und Tiefdruckgebiete, ähnlich oder wesentlich verschieden?
(Lokale Wirbelstärke).
-
Der Sonnenteich (Solar Pond) und seine Realisierungen.
-
Wie würde man magnetische Monopole nachweisen?
-
Sollte man als Schwindelfreier lieber in einem eckigen oder runden Faß
den Niagrafall hinuntertreiben (ohne Experiment).
-
Themen und Arbeitsanforderungen anderer Physik-Erstsemester in der Welt.
-
Die Schwierigkeiten des Radfahrens: Kreisfahren, bergabfahren.
Die Ausarbeitungen der Vortragenden sollen hier dann eingebunden werden.
Alle diese Themen sind bereits mit früheren Erstsemestern erprobt worden.
In der Theorie des Meßprozesses der Physik haben sich die
Arbeitsschritte bewährt:
-
sprachliche Formulierung der Fragestellung
(als Beispiele mögen die Themen des
Proseminars gelten),
-
Sammeln sogenannter vorwissenschaftlicher Erfahrungen,
also Material zusammentragen, das relevant sein könnte, Erfahrungsregeln,
Berichte Dritter,.,
-
Bildung physikalischer Begriffe,
-
idealisierte Abbildung auf mathematische Objekte,
-
Übertragung von experimentellen Relationen,
-
Kondensieren zu einer widerspruchsfreien Theorie mit Vorhersagekraft,
-
Prüfung durch Experimente.
Als Beispiel wenden wir uns den Fallversuchen am schiefen Turm von Pisa zu.
Ein Stein werde vom obersten Geländer fallen gelassen und man messe, wieviel später
er unten ankommt.
In der Schule haben wir gelernt, daß sich
die Zeitdauer taus der Fallhöhe H durch die
Auflösung der Gleichung
berechnet.
Dabei wird für g der Wert der Erdbeschleunigung in der Gegend von Pisa eingesetzt.
In einer anderen Schule wird die 'Newtonsche Gleichung' gelehrt6,
|
m dtt H = m d 2 H/d 2t = -m g .
|
(2) |
Dabei sei H die Fallhöhe zur beliebigen Zeit t, die natürlich zwischen 0,
dem Start des Experimentes und t1, dem Stop des Experimentes liegen muß.
Sodann wird diese Gleichung zweimal integriert,
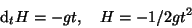 |
(3) |
und nun wird in diesen allgemeinen Fall der spezielle Wert der
Fallhöhe des Pisaturms
eingesetzt, und man erhält t=t1.
Man beachte diese in der Physik häufige schlampige
Verwendung7.
Wieder Andere ziehen vor, denselben physikalischen Prozeß
durch
die Rechenvorschrift
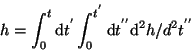 |
(4) |
zu formulieren. Man berechne die beiden Integrale nacheinander,
setze vorher für die zweite Ableitung von h nach t die
Gravitationskonstante g ein, sowie für die ja noch beliebige Zeit
t den speziellen Wert t1 der Aufprallzeit des Steines am Boden.
Wieder ein anderes, und dem Leser, der Leserin zunächst reichlich
umständliches erscheinendes, Verfahren wurde von R.P. Feynman gegeben.
Es beleuchtet besonders didaktisch die entscheidende Erkenntnis
der Naturwissenschaft über das Meßbare an einer solchen
Fallkurve, und das Nichtmeßbare.. .
Es sei hier also kurz geschildert:
Gemessen hat Newton den berühmten Apfel am Baum vor
dem Fall (optische Messung), und nach dem Fall
(Impuls- und Energiemessung beim Aufschlagen).
Dazwischen hat er angenommen, daß der Apfel einer
Bahn
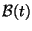 folgt. Wir verzichten nun darauf,
etwas anzunehmen, was nicht gemessen wurde, und teilen den zeitlichen
Ablauf auf in drei Zeitabschnitte:
folgt. Wir verzichten nun darauf,
etwas anzunehmen, was nicht gemessen wurde, und teilen den zeitlichen
Ablauf auf in drei Zeitabschnitte:
- die Meßzeit '=0, beim Start des Vorgangs,
- das Zeitintervall
0 < t' < t',
- und die Meßzeit t'= t des Aufpralls.
Wir verzichten nun darauf, eine bestimmte Bahn in dem Zwischenintervall
zu vermuten, oder ungemessen anzunehmen, daß
physikalische Erhaltungssätze zwischen den Messungen
gelten würden.
Wir führen den Begriff der Wirkungsdichte L ein:
(Dimension: Arbeit mal Zeit) und definieren
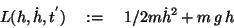 |
(5) |
(Kinetische minus potentielle Energie).
Integriert über irgendeine gedachte Bahn zwischen
den beiden Meßpunkten
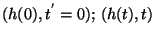 ergibt dies die Wirkung der gedachten Bahn.
Feynman's Vorschlag ist nun, daß jede mechanisch am
Aufschlagsort meßbare Größe, z.B. die 'Bahnlänge',
sich berechnen lassen durch Multiplikation des Wertes der
Bahnlänge mit dem 'Straf-Faktor'
ergibt dies die Wirkung der gedachten Bahn.
Feynman's Vorschlag ist nun, daß jede mechanisch am
Aufschlagsort meßbare Größe, z.B. die 'Bahnlänge',
sich berechnen lassen durch Multiplikation des Wertes der
Bahnlänge mit dem 'Straf-Faktor'
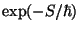 für irgendeine gegebene Bahn und Aufsummieren dieser
Produkte über alle denkbaren Bahnen, -inklusive
solcher, die Loopings und Bahnschleifen enthalten, und die Summe
dividiert durch die Zahl verwendeten Pfade8
.
Dieser genialische Vorschlag funktioniert für alle
mechanischen Messungen exakt und perfekt.
für irgendeine gegebene Bahn und Aufsummieren dieser
Produkte über alle denkbaren Bahnen, -inklusive
solcher, die Loopings und Bahnschleifen enthalten, und die Summe
dividiert durch die Zahl verwendeten Pfade8
.
Dieser genialische Vorschlag funktioniert für alle
mechanischen Messungen exakt und perfekt.
Zum Glück für Newton hat eine genaue Nachmessung des
Apfelexperimentes mit sehr viel leichteren und kleineren Teilchen
(z.B. Elektronen) ergeben, daß die hier eingeführte
Maßeinheit hbar sehr klein ist, -etwas 10-27ergsec,
sodaß für Äpfel die Annahme einer Bahn eine
sehr tüchtige Näherung bleibt,- nur hätte Newton so
gedacht, wie hier beschrieben, hätte er die aus heutiger Sicht
korrekte Mechanik bereits entdeckt,- und der Physik einen langen
Umweg
erspart.910
Diese verschiedenen Formulierungen und Rechenvorschriften mögen
zufällig erscheinen und redundant.
Das Berechnen steht aber eben nicht im Vordergrund, das überlassen wir
Rechenmaschinen, sondern die Idealisierung, Präzisierung und
Verallgemeinerung der Strukturen und Vorgehensweisen, sodaß
Vorhersagen für eine möglichst weite Klasse von Experimenten
möglich wird. Von den o.g. Gleichungen ist das nur sehr eingeschränkt
zu erwarten.
In der Physik werden Erkenntnisse ('Wahrheiten') durch
reale Experimente mit realen Apparaten an realen System
mittels
realer Personen als Experimentatoren gewonnen mit dem Ergebnis
realer (rationaler) Zahlen.
Satz 1:
Ein physikalischer Begriff wird eingeführt durch
die Angabe einer realisierbaren Bauvorschrift zusammen mit
der Angabe eines Iterationsverfahrens, mittels dessen jeweils bei
Vorlage einer gegebenen Realisierung einer Apparatur die nächste
in einer Reihe zunehmend besserer Realisierungen des
Begriffes erstellt werden kann, sowie schließlich die Abstraktion
der Baureihe aus endlich vielen immer feineren Realisierungen zum Limes
nach unendlich vielen Schritten.
Diesem Limes der Baureihe der Apparatur wird ein mathematisches Objekt
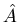 zugeordnet.
zugeordnet.
Eine Physikalische Apparatur ist definiert durch eine Baureihe von
realen (realisierbaren) Apparaturen, die aus einer vorgelegten groben Urform
durch eine Verfeinerungsvorschrift hervorgehen. Dem Limes dieser Folge
wird das mathematische Objekt 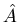 zugeordnet.
zugeordnet.
Es ist experimentell wichtig, daß die Realisierungen der Apparatur
nicht im Labor übertrieben werden, daß also rechtzeitig und nach
endlich vielen Schritten der Satz der ersten Glieder dieser Baureihe
beendet wird (wenn nicht vorher das Geld ausgeht) und die Idealisierung,
die Abstraktion gedanklich durchgeführt wird.
Die mathematischen Objekte, die physikalischen Begriffen entsprechen,
nennt man in der Mathematik auch hermitesche Operatoren, deren
Eigenschaften damit dort nachlesbar sind.
Jeder physikalische Apparat hat eine Reihe möglicher verschiedener
Zustände. Jedem Zustand der Idealisierung, dem Limes einer Baureihe
eines Apparates ordnen wir ein mathematisches Objekt
 zu.
Dabei ist
i=1,2,3,4.. ein Laufindex, der diese
Zustände der Reihe
nach abzählt. Sie sind sicher abzählbar, da sie der Experimentator
nur der Reihe nach realisieren kann. Dabei numeriert er seine Versuche durch,
und mag sie danach dann nach der Größe der Zahlen ordnen.
Sie bleiben aber abzählbar.
zu.
Dabei ist
i=1,2,3,4.. ein Laufindex, der diese
Zustände der Reihe
nach abzählt. Sie sind sicher abzählbar, da sie der Experimentator
nur der Reihe nach realisieren kann. Dabei numeriert er seine Versuche durch,
und mag sie danach dann nach der Größe der Zahlen ordnen.
Sie bleiben aber abzählbar.
Es gibt Operatoren mit wenigen verschiedenen Zuständen
Eine Meßapparatur, die mißt, ob eine Probe nass
ist, hat nur zwei Zustánde,
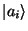 und
und
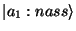 .
Analog für Apparaturen, die messen, ob es warm ist, regnet, windig ist, pp.
Andere Apparatetypen haben aber wesentlich mehr Zustände, z.B.
wenn
.
Analog für Apparaturen, die messen, ob es warm ist, regnet, windig ist, pp.
Andere Apparatetypen haben aber wesentlich mehr Zustände, z.B.
wenn 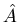 messen soll, wie schwer eine Probe ist, dann gibt es,
-nach vielen aber endlich vielen Versuchen mit verschiedenen Probematerialien,
jedenfalls durchnumerierbare aber eben doch sehr viele,
abzählbar unendlich viele verschiedene Zustände der Apparatur.
Zu jedem dieser Zustände gehört eine rationale Maßzahl, das
Ergebnis der Messung.
messen soll, wie schwer eine Probe ist, dann gibt es,
-nach vielen aber endlich vielen Versuchen mit verschiedenen Probematerialien,
jedenfalls durchnumerierbare aber eben doch sehr viele,
abzählbar unendlich viele verschiedene Zustände der Apparatur.
Zu jedem dieser Zustände gehört eine rationale Maßzahl, das
Ergebnis der Messung.
Ein physikalisches System ist eine Apparatur, an der eine Messung
durchgeführt wird, über die man etwas wissen will.
Die Messung der Dichte eines Bleiklotzes setzt eben dier Realisierung des
Bleiklotzes voraus.
Physikalische Systeme werden nun ebenfalls wie Apparturen durch
Bau- plus Verfeinerungsvorschrift und Limesbildung definiert.
Physikalische Systemen ordnen wir das mathematisch Objekt 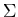 zu.
Ein solches System hat ebenfalls verschiedene Zustände.
Offensichtlich gibt es ein
zu.
Ein solches System hat ebenfalls verschiedene Zustände.
Offensichtlich gibt es ein
Dualitätsprinzip: Jeder physikalische Apparat ist auch ein
physikalisches System und umgekehrt.
Eine Messung heißt also, einen Apparat in einem vorgegebenen Zustand
auf ein physikalisches System loszulassen, dessen Zustand vor der Messung in
einen i.a. anderen Zustand nach der Messung überführt hat.
Das Dualitätprinzip hat nun aber eine (für manche Leser überraschende)
Konsequenz:
Bei einer Messung werden Apparat und System, an dem die Messung ausgeführt wird,
beide in jeweils einen neuen Zustand überführt.
Anders gesagt: Bei einem Experiment gibt es keine Ursache und Wirkung, sondern
die Auswahl, was Ursache und was Wirkung ist, bleibt der Willkühr des
Exeriment-Protokollanten überlassen. Das Experiment besagt nur:
Der Apparat 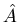 und das System
und das System 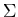 sind beide in neuen Zuständen.
11
sind beide in neuen Zuständen.
11
Satz 2: In der Physik gibt es keinen Ursache-Wirkungszusammenhang
sondern nur Experimente mit physikalischen Apparaten und Systemen
unter Beachtung ihres Dualitätsprinzips..
Wir unterscheiden die Abbildung 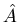 ,
das Urbild
,
das Urbild
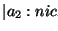 und das Abbild
und das Abbild
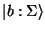 .
Parallel ändert sich entsprechend
der Dualität auch der Zustand von
.
Parallel ändert sich entsprechend
der Dualität auch der Zustand von 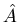 auf Grund der Einwirkung von
auf Grund der Einwirkung von 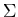 als Apparat..
als Apparat..
Einen Sonderfall wollen wir vermerken: Nehmen wir an, die Messung der
Eigenschaft a mittels der Einwirkung der Apparatur 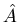 auf
auf
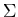 bringt keine Änderung des Zustandes von
bringt keine Änderung des Zustandes von 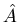 und damit auch von
und damit auch von
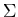 .
Dann nennt man solche Zustände auch Eigenzustände des Operators
.
Dann nennt man solche Zustände auch Eigenzustände des Operators 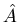 .
Liegt ein Eigenzustand vor bezüglich des Versuches der Messung mittels des
Apparates
.
Liegt ein Eigenzustand vor bezüglich des Versuches der Messung mittels des
Apparates 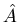 ,
so läßt sich nicht feststellen, ob überhaupt eine Messung stattgefunden hat.
Bekannte Beispiele sind natürlich: Sei der Apparat 'Geldausgeben'
auf das System 'Portemonaie' angewandt. Er ändert i.a. den Zustand des
Portmonaies. Nicht jedoch, wenn das Portemonaie im Zustand 'leer' ist.
Wir sagen also: ''ein leeres Portemonaie ist Eigenzustand zum Operator
Geldausgeben''. Wir bemerken dann nicht durch Hineinschauen, ob gerade
Geld ausgegeben wird oder nicht..
12
,
so läßt sich nicht feststellen, ob überhaupt eine Messung stattgefunden hat.
Bekannte Beispiele sind natürlich: Sei der Apparat 'Geldausgeben'
auf das System 'Portemonaie' angewandt. Er ändert i.a. den Zustand des
Portmonaies. Nicht jedoch, wenn das Portemonaie im Zustand 'leer' ist.
Wir sagen also: ''ein leeres Portemonaie ist Eigenzustand zum Operator
Geldausgeben''. Wir bemerken dann nicht durch Hineinschauen, ob gerade
Geld ausgegeben wird oder nicht..
12
Die13
physikalische RaumZeit müssen wir nun mit den
eingeschränkten Mitteln der Theorie des physikalischen
Meßprozesses erforschen.
Dieser Prozeß wird iterativ sein und uns schließlich hart
an den Rand aktueller Forschung führen.
Doch gemach.
Als vorwissenschaftliche Erfahrungen mögen genannt werden:
- es gibt 'materielle Körper' (mK), Tisch, Tafel, Stuhl, ..
manchmal werden sie auch etwas vage 'mechanische Objekte' genannt.
- mK lassen sich bewegen, verbiegen, teilen, aneinandersetzen.
Physikalisches System 'Faden':
Wir kaufen uns ein Seil. Wir bestellen (als Iterationsvorschrift) ein
neues Seil 'deutlich dünner und länger'. dies wiederholen wir solange
nacheinander, bis
der Händler nicht mehr liefern oder wir es nicht bezahlen können.
Die weiteren Iterationsschritte nehmen wir gedanklich vor.
Den Limes nach unendlich vielen Schritten bezeichnen wir als Faden und
ordnen ihm ein mathematisches Objekt 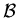 zu.
zu.
Wir kaufen uns ein Tintenfaß und einen Pinsel. Mit diesem markieren
wir auf einem Faden drei mit diesen Mitteln herstellbare
möglichst nahe benachbarte Flecke.
Als Iterationsschritt kaufen wir schrittweise feinere Pinsel, soweit
dies möglich ist.
Den idealisierten Grenzwert der drei benachbarten Flecken auf dem Faden nennen
wir Nachbarschaftsbeziehung. Den mittleren Punkt nennen wir im
folgenden 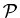 ,
die beiden anderen Punkte,
die auf derselben Kurve liegen, sind durch den Punkt
,
die beiden anderen Punkte,
die auf derselben Kurve liegen, sind durch den Punkt
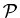 getrennt. Von jedem dieser beiden Nachbarpunkte aus erscheint der
andere hinter
getrennt. Von jedem dieser beiden Nachbarpunkte aus erscheint der
andere hinter 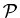 ,
er selbst sieht
sich natürlich vor
,
er selbst sieht
sich natürlich vor
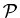 .
Diese eindeutige
'Vor/Hinter Beziehung' der drei Punkte nennt man auch
eine orientierte eindimensionale Nachbarschaftsbeziehung
(d.h., wenn man eine Kurve durch
.
Diese eindeutige
'Vor/Hinter Beziehung' der drei Punkte nennt man auch
eine orientierte eindimensionale Nachbarschaftsbeziehung
(d.h., wenn man eine Kurve durch 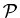 zieht,
dann trennt dieser die Punkte davor von den
Punkten dahinter.
zieht,
dann trennt dieser die Punkte davor von den
Punkten dahinter.
Zeichnung
Wir haben also nun den Faden mit einer eindimensionalen orientierten
Punktmannigfaltigkeit mit Orientierung ausgerüstet.
Diese Orientierung erlaubt es nun, auf dem Faden entlang zu wandern:
von 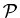 zum Nachbarpunkt
zum Nachbarpunkt
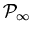 vor
vor 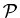 ,
von diesem zu
seinem Nachbarpunkt 'vor
,
von diesem zu
seinem Nachbarpunkt 'vor
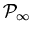 ,
also
,
also
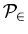 ,
und so fort.
Eine Änderung der Nachbarschaftseigenschaften auf unserer Wanderung stellen
wir nicht fest.
Wir ordnen daher der orientierten Punktmenge
,
und so fort.
Eine Änderung der Nachbarschaftseigenschaften auf unserer Wanderung stellen
wir nicht fest.
Wir ordnen daher der orientierten Punktmenge 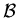 die Menge der reellen
Zahlen zu. Diese Abbildung kann auf vielfältige Weise erfolgen,
(welche Zahl ordne ich dem Punkt
die Menge der reellen
Zahlen zu. Diese Abbildung kann auf vielfältige Weise erfolgen,
(welche Zahl ordne ich dem Punkt 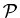 zu, für die Wahl der Zahl
für
zu, für die Wahl der Zahl
für
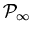 habe ich jede Freiheit, sofern sie nur größer ist
als die für
habe ich jede Freiheit, sofern sie nur größer ist
als die für  ), es kommt also auf die Abbildung der Orientierung
und der Nachbarschaft an, nicht auf die aktuellen Zahlen.
Eine solche Abbildung heißt auch
affine Abbildung.
Beispiele solcher affinen eindimensionalen Zusammenhänge sind
die 'wärmer/kälter' Relation in der Thermodynamik,
'schwerer/leichter' in der Mechanik, 'weniger/mehr elektrisch geladen'
in der Elektrodynamik.
), es kommt also auf die Abbildung der Orientierung
und der Nachbarschaft an, nicht auf die aktuellen Zahlen.
Eine solche Abbildung heißt auch
affine Abbildung.
Beispiele solcher affinen eindimensionalen Zusammenhänge sind
die 'wärmer/kälter' Relation in der Thermodynamik,
'schwerer/leichter' in der Mechanik, 'weniger/mehr elektrisch geladen'
in der Elektrodynamik.
Wir erfahren also auf unserem Faden  ,
daß
kein Punkt vor dem anderen ausgezeichnet ist
(Isotropie des Raumes) und daß überall die gleichen
Nachbarschaftsbeziehungen gelten (Homogenität des Raumes,
zwei grundlegende Eigenschaften des Physikalischen Raumes.
,
daß
kein Punkt vor dem anderen ausgezeichnet ist
(Isotropie des Raumes) und daß überall die gleichen
Nachbarschaftsbeziehungen gelten (Homogenität des Raumes,
zwei grundlegende Eigenschaften des Physikalischen Raumes.
Eine weitere Erkenntnis ist, daß physikalische RaumZeit-Eigenschaften
nur insofern definiert sind, wie sie mit materiellen Körpern ausmeßbar
sind, - ohne Materie wäre also die RaumZeit nicht ausmeßbar.
Bei einer Bewegung des Fadens ändern sich die Nachbarschaftseigenschaften
nicht (die 'Topologie' ändert sich nicht).
Die vorwissenschaftliche Erfahrung sagt, daß mechanische Körper
'diskret' sind (voneinander unterscheidbar), aber miteinander in
Berührung/Kontakt gebracht werden können.
Wir denken uns daher nun zwei verschiedene Fäden miteinander an einem
Punkt 'festgeklebt' (fest berührt).
Erste Versuch ergeben, daß wir nun zwei Nachbarschaftsbeziehungen
zum selben Punkt, die unabhängig voneinander sind, denn schon
die Nachbarschaftspunkte sind verschieden. Auch an dieser
Eigenschaft ändert sich durch Bewegen des gekreuzten Fadenpaares
nichts.
Als Nächstes kaufen wir uns einen guten Vorrat an Fäden und versuchen,
sie so eng wie möglich aneinander zu schmiegen. Dies geschieht wiederum
iterativ. Seile lassen sich sehr gut eng nebeneinander auf dem Boden auslegen.
Daran ändert sich auch nichts, wenn wir zu feineren Seilen übergehen,
wenn wir den 'parallelen' Fadensatz verbiegen. Diese parallele
Schichtung ist ebenfalls unabhängig von der gemeinsamen Bewegung im 'Raum',
von Verbiegungen, Streckungen, Stauchungen.
Nun nehmen wir zwei solcher Fadensätze und kleben sie zu einem
Fadennetz, auch Haarnetz genannt.
Die genaue Klebevorschrift ist:
Klebe einen Faden von Satz 2 an Punkt  von Satz 1.
Nun gehe längs Faden aus Satz 1 durch
von Satz 1.
Nun gehe längs Faden aus Satz 1 durch  zu dem Nachbarpunkt
zu dem Nachbarpunkt
 auf Faden 1 aus Satz 1. Dort klebe den nächsten Faden von Satz 2
an.
Setze dies längs des ganzen Fadens 1 aus Satz 1 fort, bis alle Fäden aus
Satz 2 verbraucht sind.
Nun gehen wir von
auf Faden 1 aus Satz 1. Dort klebe den nächsten Faden von Satz 2
an.
Setze dies längs des ganzen Fadens 1 aus Satz 1 fort, bis alle Fäden aus
Satz 2 verbraucht sind.
Nun gehen wir von  längs des an ihm festgeklebten
Fadens aus Satz 2 zum Nachbarpunkt von
längs des an ihm festgeklebten
Fadens aus Satz 2 zum Nachbarpunkt von  auf ihm.
Dort kleben wir den nächsten Faden aus Satz 1 an.
Iterativ gelingt es so, ein Fadennetz zu erzeugen, dicht gestopft und aus
zwei gekreuzten Lagen bestehend. Jeder Faden aus Satz 1 ist nur an je einer
Stelle mit jedem Faden aus Satz 2 gestgeklebt, jedem Teppichknüpfer
wohl bekannt. Dies nennen wir ein affines zweidimensionales Fadennetz.
Mit ihm läßt sich nun gut der Raum erforschen.
Bewegungen oder Verzerrungen des
Netzes ändern die Nachbarschaftseigenschaften nicht.
auf ihm.
Dort kleben wir den nächsten Faden aus Satz 1 an.
Iterativ gelingt es so, ein Fadennetz zu erzeugen, dicht gestopft und aus
zwei gekreuzten Lagen bestehend. Jeder Faden aus Satz 1 ist nur an je einer
Stelle mit jedem Faden aus Satz 2 gestgeklebt, jedem Teppichknüpfer
wohl bekannt. Dies nennen wir ein affines zweidimensionales Fadennetz.
Mit ihm läßt sich nun gut der Raum erforschen.
Bewegungen oder Verzerrungen des
Netzes ändern die Nachbarschaftseigenschaften nicht.
Wir setzen nun diese Konstruktion fort. Wir nehmen einen dritten Fadensatz,
wiederholen die Verklebevorschrift mit den bereits verklebten ersten zwei
Fadensätzen, einen vierten, fünften, sechsten.
Dabei machen wir eine überraschende Entdeckung.
Wir können jeden Ort errreichen, wenn wir von  ausgehend,
erst längs des Fadens aus Satz 1 durch
ausgehend,
erst längs des Fadens aus Satz 1 durch  genügend weit laufen,
bis wir geeignet zu einem Faden aus einem weiteren Satz und dann aus immer
weiteren Sätzen abbiegend,
den gewünschten Ort erreichen. Überraschenderweise genügen bereits
stets nur drei Fadensätze, um jeden beliebigen Ort zu erreichen.
Daher nennen wir den Physikalischen Raum der klassischen Mechanik
dreidimensional.
Das Wandern längs eines Fadens nennen wir Paralleltransport14,
Den Paralleltransport längs eines Fadens nennen wir auch Translation
längs
genügend weit laufen,
bis wir geeignet zu einem Faden aus einem weiteren Satz und dann aus immer
weiteren Sätzen abbiegend,
den gewünschten Ort erreichen. Überraschenderweise genügen bereits
stets nur drei Fadensätze, um jeden beliebigen Ort zu erreichen.
Daher nennen wir den Physikalischen Raum der klassischen Mechanik
dreidimensional.
Das Wandern längs eines Fadens nennen wir Paralleltransport14,
Den Paralleltransport längs eines Fadens nennen wir auch Translation
längs  .
.
Die Paralleltransporte längs verschiedener Fadensätze
haben nun eine weitere überraschende Eigenschaft:
Wir gehen von einem Punkt P(i) auf dem Faden  aus Satz 1,
nennen wir ihn
aus Satz 1,
nennen wir ihn
 längs ihm zu einem Nachbarpunkt
längs ihm zu einem Nachbarpunkt
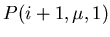 ,
dort wechseln wir auf
den Fadensatz 2, der Klebepunkt sei
,
dort wechseln wir auf
den Fadensatz 2, der Klebepunkt sei
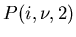 ,
wandere längs dem Faden
,
wandere längs dem Faden 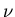 aus Satz 2 zum
Nachbarpunkt
aus Satz 2 zum
Nachbarpunkt
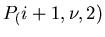 ,
gehe dort auf den dort angeklebten Faden auf Satz 1 zurück
,
gehe dort auf den dort angeklebten Faden auf Satz 1 zurück
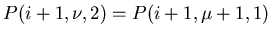 ,
dort zurück zu
,
dort zurück zu
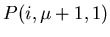 und von dort auf Fadensatz 2 zurück zum Ursprung.
Mit solchen kleinen zum Ursprung zurückkehrenden Ausflügen erfahren wir:
jeder Weg kann auch in umgekehrter Reihenfolge durchlaufen werden,
jeder dieser Ausflüge mit gleichen Schritten führt zum Ursprung
zurück, jeder Punkt im Raum ist durch Wandern auf drei solchen
verklebten Fadensätzen erreichbar. Auf den Weg im Einzelnen
(Weg in der Großstadt mit feinem Straßennetz),
kommt es nicht an.
Man nennt solche Punktmannigfaltigkeiten dreidimensional und
Abel'sch oder kommutativ, nach dem Mathematiker Abel.
und von dort auf Fadensatz 2 zurück zum Ursprung.
Mit solchen kleinen zum Ursprung zurückkehrenden Ausflügen erfahren wir:
jeder Weg kann auch in umgekehrter Reihenfolge durchlaufen werden,
jeder dieser Ausflüge mit gleichen Schritten führt zum Ursprung
zurück, jeder Punkt im Raum ist durch Wandern auf drei solchen
verklebten Fadensätzen erreichbar. Auf den Weg im Einzelnen
(Weg in der Großstadt mit feinem Straßennetz),
kommt es nicht an.
Man nennt solche Punktmannigfaltigkeiten dreidimensional und
Abel'sch oder kommutativ, nach dem Mathematiker Abel.
Ein Schritt fehlt noch und Zeichnung
Paralleltransporte im mehrdimensionalen Raum haben also eine
Verknüpfung: das Hintereinanderausführen von solchen
Transporten auf dem gleichen oder auf verschiedenen Fadensätzen.
Bezeichnen eine solche Verknüpfung mit (+) und einen Paralleltransport
längs eines Fadens in einer Richtung aus einem
Satz i mit
Ti(a), um einen Weg von einem zu einem anderen Punkt auf einem
Faden aus Satz i xu beschreiben.
Die Angabe dieser beiden Punkte nennen wir
(
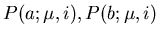 oder kurz A(a,b).
oder kurz A(a,b).
Einen Satz von Eigenschaften eines physikalischen Begriffes nennen wir
Algebra.
Die Algebra des Hintereinanderausführens von Paralleltransporten
ist leicht erfahrbar:
Es gibt einen Transport T(B) mit einem Punktepaar B(b,a),das wir auch
anschaulich mit T(-B) bezeichnen könnten,
derart daß
Ti(A) (+) Ti(B) = T(0) . Existenz eines Inversen
soll besagen, zu jedem Transport längs eines Fadens gibt es den
umgekehrten Prozeß, T(0) steht für 'man landet wieder beim
Ausgangspunkt'.
Existenz eines identischen Transports Ti(0)vo, Punkt a zum selben Punkt a:
|
Ti(A) (+) Ti(0) = Ti(A) .
|
(6) |
Transporte können vertauscht werden
|
Ti(A) (+) Tj(C) = Tj(C) (+) Ti(A).
Kommutativ-Gesetz
|
(7) |
Man kann auf nicht triviale Weise zum Ausgangspunkt zurückkehren.
|
Ti(A) (+) (Tj(B) (+) Tk(C)) = (Ti(A) (+) Tj(B)) (+) Tk(C)
Assoziativ-Gesetz
|
(8) |
Alle diese wichtigen Eigenschaften müssen wir durch Experimente
erfahren.
Der gesamte Stell15 von Eigenschaften heißt
Algebra der Verknüpfung 'Hintereinanderausführen von
Paralleltransporten. Diese bilden eine kommutative Lie-Algebra
(benannt nach dem Mathematiker Lie, weil er sich zuerst mit
Algebren befaßte, die für beliebige Punktepaare aus einer
kontinuierlichen orientierten Punktmannigfaltigkeit gilt).
Die physikalische Zeit hat eine eindimensionale Nachbarschaftsbeziehung
des 'früher, später' im Sprachgebrauch.
Jeder mechanische Faden hat in seiner Längsrichtung ein
bei der tatsächlichen experimentellen Erzeugen
('Spinnen durch eine Spinne')
eine zeitliche 'Nacheinander' Nachbarschaftsrelation aufgeprägt.
Diese können von späteren Wanderern auch nur in der gleichen
Abfolge (wenn auch verschieden schnell) durchlaufen werden.
Eine zusätzliche Komplikation ist die notwendige Erfüllung des
Kausalitätsprinzips:
die höchstmögliche Geschwindigkeit, mit der längs eines
Fadens gelaufen werden kann, ist für alle Fäden gleich und gleich
c, der Lichtgeschwindigkeit.
Dies bedingt, daß es keinen Faden mit allen seinen Punkten zu gleicher
Zeit geben kann (keine universelle 'Gleichzeitigkeit'),
während der 'Faden' zu festem Ort im Volksmund einfach Uhr
heißt und nach der Kausalität natürlich erlaubt ist,
aber zum den Raum bedeckenden Netz nichts beiträgt.
Längs eines Fadens, der einen gegebenen Punkt zu einer Start-Zeit
mit seinen
späteren Punkten verbindet (auch topologische lokale Uhr genannt).
Es ist also vollkommen problemlos, die vorgenannten Überlegungen auf
die Zeit auszudehnen und die Physikalische RaumZeit als homogenen
isotropen vierdimensionalen Raum mit den Paralleltransporten in drei
Raumdimensionen und einer Zeitdimension, also in einer vierdimensionalen
Welt zu erkennen, mit einer kommutativen Abel'schen Algebra für das
Hintereinanderausführen von Paralleltransporten.
(Auch Uhren kann man zurückstellen).
Eine algebraisch erkennbare verschiedene Unterstruktur,
etwa daß Raum und Zeit
verschiedene Eigenschaften hätten, ist nicht erkennbar.
Die RaumZeit in der Physik bildet ein homogenes vierdimensionales
isotropes Kontinuum mit einer aufgeprägten Eigenschaft für Spazierwege.
Die historische scharfe Unterscheidung von Raum und Zeit finden wir hier
nicht gerechtfertigt.
This text is
- to be used as raw material for preparing lecture notes,
- to be used by the students of second term Physics
as a guide which topics to be looked up and to be worked through
in text books,
-
to be used as a warning that German Physicists have to use the language
broken english in their aimed for professional life.
To learn a language one better starts early, and I assure the reader
that this text is written in perfect broken english,
-
not to use it instead of a textbook,
-
not to assume that by working through, one would be fit for the Physics
studying at any place or Oldenburg, - it needs to dig through
exercises.
For a mathematician this text is unreadable: few proofs, and then
only sketched, incomplete, neglecting all kinds of sophistic
subtleties, -for these we have the huge set of Algebra textbooks
developed to perfection over the decades, -and unusuable in daily
life physics, not only because of its often clumsy notations,..
- for a physicist, having worked through textbooks with titles
such as Mathematical Physics I hope at least the next edition
(in 1998) reading through will be a real pleasure..
This text (together with textbooks, exercises, ..) is aimed to
support for a student on his way to become a physicist,
to think and work algebraic,
to discover rules, recognize rules, check the consistency of rules,
think in rules, work with rules, - and thus help design, set up
and exploit experiments to transfer them to Theoretical Physics,
the language of which is Algebra, to predict successfully
new experiments, called understanding nature.
Any textbook of Linear Algebra will do, if read in comparison to
this lecture and other books.
Specifically addressing young physics students are, -apart
from some all-time classics such as D. Hilbert: Mathematische Methoden
der Physik,- and used here are the books by the highly
respected theoretical physicist S. Grossmann[],
specifically carefull with exercises and getting trained,
by the mathematician G. Behrendt[] who tries to
skip the details of proofs sometimes in favour of getting more
practical training, and the book by Dennery[],
which is most useful for those to gain a thorough background for
the theoretical physics classes to come including quantum mechanics.
A derivative of this book is the script, passed out to local students,
of R. Ebert, a theoretical physicist and R. Göbel, a mathematical
physicistsee:Skript.
We just give here an aphoristic short essay of what should be learned
elsewhere.
Physics casts nature into relations between observables.
Let the physicists do the work of addressing a specific experiment.
They
have to define the physical system in question
(by giving the physical real design in all details, and even building it
if it is not a mechanical apparatus[].
This can be learned in classes of Theory of Measuring in Physics,
Theorie des Meßprozesses, etc, and will not extensively touched
here but we need it as the necessary background what to learn Linear
Algebra for.
The above specified real definition of the Physical System in question
defines the Physical System in question. We map it to a yet
undefined alebraic quantity 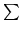 .
In Physics the to be assigned
algebraic properties are defined by properties of the real physical
system in experiments. We need the real physical experiments to learn
about the algebraic properties of
.
In Physics the to be assigned
algebraic properties are defined by properties of the real physical
system in experiments. We need the real physical experiments to learn
about the algebraic properties of 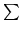 16
16
An experiment is bringing into contact (at least) two different systems
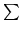 and
and 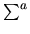 and
study (measure) their changed properties afterwards.
Such a property is recorded by reading off some gadgets.
Obivously both systems need properties to be realized at all.
Examples of properties are (colour, weight, length, height, mass, ..).
Their measurement means reading off the gadget and noting the result.
Up to now, any of the physical properties of any system have either
real
numbers for their measurement the result can be mapped to real numbers.
Examples are the height is 12 cm, the colour is green.
All possible colours can be ordered according to their frequency and
then mapped to real numbers.
Up to now, more precisely, for any physical observabele,
the set of all accessible measurements could always be mapped to the
rational numbers only. The rational numbers are any number which
can be written as a quotient of two integer numbers. Any real number
can be approximated to any wished finite accuracy by rational numbers.
The advantage is that rational numbers can be ordered such that they can be
mapped to the set of integer numbers, they are 'countable', whereas
real numbers are not countable (abzählbar).
In Quantum mechanics we will learn that there is even more
truth to it, it can be proven there that any physical property has only
a countable (though still possibly infinite) number of different
measurent values.
ootnoteWe do not go so far, although we can understand this
rgument, to eliminate all real numbers from physics at all,
as recommended by one of the most internationally respected
German Physicists, J. Ehlers, but will use for abbreviation and
elegance of writing for the ratio of the experimental measurements
of the circumference of a circle divided by its diameter the real
number
and
study (measure) their changed properties afterwards.
Such a property is recorded by reading off some gadgets.
Obivously both systems need properties to be realized at all.
Examples of properties are (colour, weight, length, height, mass, ..).
Their measurement means reading off the gadget and noting the result.
Up to now, any of the physical properties of any system have either
real
numbers for their measurement the result can be mapped to real numbers.
Examples are the height is 12 cm, the colour is green.
All possible colours can be ordered according to their frequency and
then mapped to real numbers.
Up to now, more precisely, for any physical observabele,
the set of all accessible measurements could always be mapped to the
rational numbers only. The rational numbers are any number which
can be written as a quotient of two integer numbers. Any real number
can be approximated to any wished finite accuracy by rational numbers.
The advantage is that rational numbers can be ordered such that they can be
mapped to the set of integer numbers, they are 'countable', whereas
real numbers are not countable (abzählbar).
In Quantum mechanics we will learn that there is even more
truth to it, it can be proven there that any physical property has only
a countable (though still possibly infinite) number of different
measurent values.
ootnoteWe do not go so far, although we can understand this
rgument, to eliminate all real numbers from physics at all,
as recommended by one of the most internationally respected
German Physicists, J. Ehlers, but will use for abbreviation and
elegance of writing for the ratio of the experimental measurements
of the circumference of a circle divided by its diameter the real
number 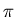 ,..
,..
In measuring with a system 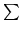 the properties of another system
the properties of another system
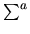 by reading off the gadgets for measuring the properties
of
by reading off the gadgets for measuring the properties
of 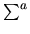 we are beware of course of one specific case:
let us assume the gadget y had the value 3.1 before, and shows
after the measurement the same value. Then we really do not know,
has there has been an experiment with contact to
we are beware of course of one specific case:
let us assume the gadget y had the value 3.1 before, and shows
after the measurement the same value. Then we really do not know,
has there has been an experiment with contact to 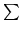 at all or not.
Such a state we call an eigenstate of
at all or not.
Such a state we call an eigenstate of 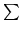 with regard to y of
with regard to y of
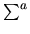 .
.
To summarize:
-
A Physical system is defined by building it in reality and noting
the respective description of construction.
-
Its states of possible realization are given by measuring
(with the respective apparatuses (other systems) attached),
the actual values of its attributes, called measured values
. In physics, attributes are called observables.
- Measured values proved in physics experiments to be always
real (more precisely rational).
-
Mathematics serves us with a special class of operators the eigenvalues
of them are always real , the Hermitean operators. We thus will explore
their algebra and test whether they suit to work as representative of
a measuring apparatus, and because of the symmetry of apparatus and
system for a physical system.
-
The mesuring results have to be recorded and reported. This might be
done as it suits the reader, in his language.
Thus we may need translation codes into different languages or
representations.
We thus need mathematical constructs, transformations, which
ar to do the job but do not and by no means change or even reduce
the information content, the physical information.
They are to do the transformation to any conceivable understandable
language with the full original information.
Mathematics serves us with a certain class of operators which
do just this: the unitary transformations. This will be the second
class of mathematical objects we will study specifically.
Dies ist eine einfache Einführung in
das elementare Rüstzeug, um physikalische Aussagen mit mathematischen
Mitteln darzustellen und mitzuteilen.
Wir werden auf alle mathematischen Sonderfälle, Verallgemeinerungen,
Weiterungen etc. verzichten, um den Einstieg in die Anschauung als
Physiker zu gewinnen: einfache Beispiele üben, bis sich die Anschauung
einstellt, und DANN mit den Mathematikern reden (oder sie lesen).
Die Anforderungen an mathematisches Rüstzeug für die Physik sind:
17
-
Es muß einfach zu merken und zu handhaben sein,
-
es muß die Phantasie und Vorstellung unterstützen,
-
es sollte nur mit meßbaren Zahlen hantiert werden,
-
diese müssen unabhängig von der Wahl der Koordinaten der Darstellung
sein,
-
die Formeln und Regeln sollten in allen Dimensionen gleich ausschauen.
Das einfache gewöhnliche eindimensionale Integral wollen wir so umformulieren,
daß die Beschreibung den o.g. Anforderungen genügt.
Gegeben sei also eine gewöhnliche Funktion f(x) mit
![$x \in [a,b]$](img32.gif) ,
die integriert werden kann zu
,
die integriert werden kann zu
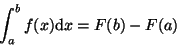 |
(9) |
Die einzelnen Bausteine dieser Formulierung sind
das Grundgebiet, das Integral und der Integrand.
![$x \in [a,b]$](img32.gif) ist die Menge aller Punkte vom
Anfangspunkt a zum Endpunkt b. Es ist eine eindimensionale
orientierte einfach zusammenhängende 'Punktmannigfaltigkeit,
die durch das kalligraphische Symbol
ist die Menge aller Punkte vom
Anfangspunkt a zum Endpunkt b. Es ist eine eindimensionale
orientierte einfach zusammenhängende 'Punktmannigfaltigkeit,
die durch das kalligraphische Symbol
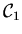 bezeichnet wird,
der Index gibt die Dimension an, hier ist es eine
eindimensionales Streckenstück.
Jeder Punkt im Innern dieser Punktmenge hat einen unmittelbar 'vor' ihm
liegenden und einen unmittelbar 'hinter' ihm liegenden Punkt in unmittelbarer
Nachbarschaft (aus der Sicht der Wanderung von a nach b).
bezeichnet wird,
der Index gibt die Dimension an, hier ist es eine
eindimensionales Streckenstück.
Jeder Punkt im Innern dieser Punktmenge hat einen unmittelbar 'vor' ihm
liegenden und einen unmittelbar 'hinter' ihm liegenden Punkt in unmittelbarer
Nachbarschaft (aus der Sicht der Wanderung von a nach b).
Die beiden Randpunkte zeichnen sich dadurch aus, daß sie
auf der x-Achse in unmittelbarer Nachbarschaft vor/hinter sich einen
Punkt aus
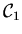 und auf der entgegengesetzten Seite einen Punkt in der
unmitelbaren Nachbarschaft, der NICHT zu
und auf der entgegengesetzten Seite einen Punkt in der
unmitelbaren Nachbarschaft, der NICHT zu
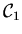 gehört.
Solche Punkte heißen Randpunkte, sie bilden selbst
eine orientierte, wenn auch 'Null-dimensionale' (nur isolierte Punkte)
Punktmenge
gehört.
Solche Punkte heißen Randpunkte, sie bilden selbst
eine orientierte, wenn auch 'Null-dimensionale' (nur isolierte Punkte)
Punktmenge
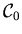 ,
mit der besonderen Eigenschaft
Rand von
,
mit der besonderen Eigenschaft
Rand von
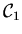 zu sein. Wir bezeichnen dies als
zu sein. Wir bezeichnen dies als
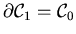
Diese beiden Randpunkte, die
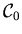 bilden, sind in ihren
Nachbarschaftseigenschaften alle gleichartig, es gibt
keine besonderen Randpunkte von der Randpunktmenge von
bilden, sind in ihren
Nachbarschaftseigenschaften alle gleichartig, es gibt
keine besonderen Randpunkte von der Randpunktmenge von
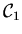 .
.
Diese Beobachtung fassen wir nun im Satz von Columbus18
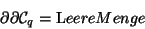 |
(10) |
Dieser Satz gilt f jede ür beliebige einfach
zusammenhängende,
orientierte, q-dimensionale Punktmannigfaltigkeit im n-dimensionalen
Raum (natürlich ist
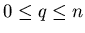 ).
Das Integral stellt man sich ja meist ebenso
anschaulich wie umständlich als Vorschrift vor:
Eindimensional: nimm die Strecke
).
Das Integral stellt man sich ja meist ebenso
anschaulich wie umständlich als Vorschrift vor:
Eindimensional: nimm die Strecke
![$x \in [a,b]$](img32.gif) ,
teile sie in Ngleiche Intervalle der Intervall-Länge
,
teile sie in Ngleiche Intervalle der Intervall-Länge
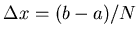 ,
nimm irgendein x aus einem Intervall, berechne für dieses den
Funktionswert f(x), multipliziere beide,
,
nimm irgendein x aus einem Intervall, berechne für dieses den
Funktionswert f(x), multipliziere beide,
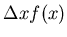 und
addiere die so gewonnenen Beiträge
aus allen Intervallen. Vom Resultat, dem
Summenwert bilde schließlich den Limes
und
addiere die so gewonnenen Beiträge
aus allen Intervallen. Vom Resultat, dem
Summenwert bilde schließlich den Limes
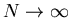 des Summationsergebnisses,- und lehne Dich erschöpft zurück,
des Summationsergebnisses,- und lehne Dich erschöpft zurück,
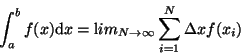 |
(11) |
Klarer formuliert und für ein q-dimensionales Grundgebiet
heißt das doch:
nimm jeden Punkt aus der Grundmenge
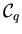 und berechne den
Integranden, summiere dann alle Beiträge auf.
und berechne den
Integranden, summiere dann alle Beiträge auf.
Die numerische Realisierung bleibt dem Leser überlassen
(Näherung durch Einteilung von
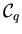 in q-dimensionale kleine
'infinitesimale' Gebiete19
und jeweils Berechnung
von f(x)).
Diese ganze Vorschrift wird durch das Summationszeichen beschrieben:
in q-dimensionale kleine
'infinitesimale' Gebiete19
und jeweils Berechnung
von f(x)).
Diese ganze Vorschrift wird durch das Summationszeichen beschrieben:
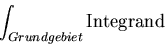 |
(12) |
f(x) d x werde durch f (ohne Argument) abgekürzt:
Falls das Integral erfolgreich berechnet werden konnte, gab es eine
Funktion F(x), deren Differential
(d /d x) F =f(x) wir nun
mit 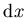 multiplizieren und so
multiplizieren und so
erhalten.
f läßt sich integrieren, wenn es eine Funktion F gibt, mit
d F=f.
Da wir ja nicht viel über die Menge der denkbaren Funktionen f(x)
verraten haben, ist durchaus denkbar, daß F wiederum integrierbar ist,
d.h. daß es wiederum eine Funktion
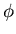 gibt mit
gibt mit
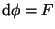 .
Hintereinander geschrieben kann jeder Leser (so hoffe ich doch),
die zweifache Integration einer nicht näher
erläuterten Funktion fleicht selbst durchführen, stimmts?
.
Hintereinander geschrieben kann jeder Leser (so hoffe ich doch),
die zweifache Integration einer nicht näher
erläuterten Funktion fleicht selbst durchführen, stimmts?
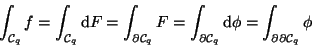 |
(15) |
Netter geschrieben ergibt dies, da ja
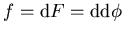 ist,
die Äquivalenz
ist,
die Äquivalenz
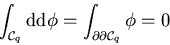 |
(16) |
denn eine Summe zu bilden aus keinem Summanden (die Punktmenge
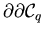 ist ja die leere Menge) besteht, ist natürlich
Null20
ist ja die leere Menge) besteht, ist natürlich
Null20
Damit haben wir eine tiefliegende Äquivalenz zwischen der
Integrationsgrundgebiets-Aussage
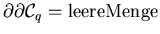 und der differentiellen Aussage 'das Differential d zweimal angewendet
auf einen beliebigen Integranden ergibt stets die
Null',
und der differentiellen Aussage 'das Differential d zweimal angewendet
auf einen beliebigen Integranden ergibt stets die
Null',
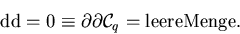 |
(17) |
Diese schöne Aussage werden wir gleich vertiefen.
Zunächst aber schreiben wir das Ergebnis dieses Kapitels an, das
Integral für eine Dimension:
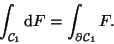 |
(18) |
Ersichtlich erfüllt diese Darstellung des einfachen eindimensionalen
Integrals
(in der üblichen Schreibweise
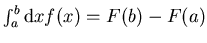 sähe
man das nicht),
alle Anforderungen an ein gutes Rüstzeug, denn für
beliebige Dimension
sähe
man das nicht),
alle Anforderungen an ein gutes Rüstzeug, denn für
beliebige Dimension 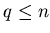 eines orientierten Integrationsgrundgebietes
eines orientierten Integrationsgrundgebietes
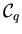 sieht es formäquivalent aus:
sieht es formäquivalent aus:
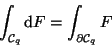 |
(19) |
Wir müssen nun nur noch üben, welche Integrandentypen es in der Physik
in den verschiedenen Dimensionen geben kann.
21
Die Integranden sind je eine Zahl für jeden Punkt aus der Grundmenge
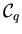 ,
fertig zur Aufsummation.
Die
Darstellung der mathematischen Inhalte mittels Integranden und ihrer
Integration über orientierte Punktmannigfaltigkeiten erfüllt alle unsere
Forderungen an ein sinnvolles und effektives Rüstzeug.
Weder gehen für die Darstellung Koordinaten ein, noch sind die Formeln
abhängig von der Dimensionszahl des Raumes oder der Integrationsgrundmenge.
Vor Einführung dieser Darstellung durch Cartan[]
etwa 1940 war je nach Dimension des Grundgebietes und des Raumes ein eigener
mathematischer Satz notwendig, benannt nach ihren Entdeckern, z.B. Green,
Stokes, Gauß. Daher wird der Integrationssatz [] auch manchmal
Satz zur Integration von Green-Stokes-Gauß genannt.
22
,
fertig zur Aufsummation.
Die
Darstellung der mathematischen Inhalte mittels Integranden und ihrer
Integration über orientierte Punktmannigfaltigkeiten erfüllt alle unsere
Forderungen an ein sinnvolles und effektives Rüstzeug.
Weder gehen für die Darstellung Koordinaten ein, noch sind die Formeln
abhängig von der Dimensionszahl des Raumes oder der Integrationsgrundmenge.
Vor Einführung dieser Darstellung durch Cartan[]
etwa 1940 war je nach Dimension des Grundgebietes und des Raumes ein eigener
mathematischer Satz notwendig, benannt nach ihren Entdeckern, z.B. Green,
Stokes, Gauß. Daher wird der Integrationssatz [] auch manchmal
Satz zur Integration von Green-Stokes-Gauß genannt.
22
Hier folgen Beispiele für die
üblichen
Schreibweisen Green Stokes Gauss
Dieses Kapitel zeigt, wie verschiedene in der Physik
gebräuchliche Objekte (Skalare, Vektoren,
Tensoren,.. ) in Integranden eingehen können.
Danach lassen sich vom Leser oder Leserin alle Skripten zur
Einführung der Physik unter konsequenter Vewendung von Integranden
umschreiben. Sie werden damit wesentlich
verständlicher, wesentlich einfacher und anschaulicher.
In der Physik treten nur Objekte auf, deren mathematische Darstellung sich
unter Koordinatentransformationen verhalten wie
Skalare (Zahlenwert unabhängig von der Koordiantenwahl), Vektoren oder
Tensoren.
Aus ihnen lassen sich jeweils Skalare bilden durch Skalarprodukte mit einem
anderen Vektor.
Wie treten nun physikalische Objekte in Integranden auf?
Zum einen hatten wir ein Obkjekt F, zahlenwertig und nur an den
isolierten Randpunkten einer eindimensionalen Grundmenge aufzusummieren,
diese nennen wir eine 0-Form, die Bezeichnung wird gleich suggestiver
werden.
Eine Funktion, die zu jedem Raumpunkt einer Grundmenge
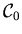 einen
Zahlenwert ausgibt, nennt man auch Skalarfeld
(' an jedem Raumpunkt ist ein (koordinatenunabängiger) Skalar angeheftet.
Manchmal heften wir zur Erläuterung den Index Null an,
F0).
einen
Zahlenwert ausgibt, nennt man auch Skalarfeld
(' an jedem Raumpunkt ist ein (koordinatenunabängiger) Skalar angeheftet.
Manchmal heften wir zur Erläuterung den Index Null an,
F0).
Das Integral über eine eindimensionale Grundmenge (Intervall auf einer
Kurve oder Strecke) war im  eine gewöhnliche Funktion
f(x), der Integrand also
eine gewöhnliche Funktion
f(x), der Integrand also
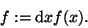 |
(20) |
Einen solchen Integrandentyp
nennen wir 1-Form, weil in ihm ein Differential
d x
auftritt.
Als Skalarprodukt ist f leichter in einem Raum höherer Dimension
zu erkennen: Im
 ist der Integrand eines Integrals über
der Grundmenge eines eindimensionalen Kurvenstücks
ist der Integrand eines Integrals über
der Grundmenge eines eindimensionalen Kurvenstücks
 ein
Skalarprodukt eines Vektorfeldes mit einem 'Differentialvektor'.
Beide seien nun erläutert.
ein
Skalarprodukt eines Vektorfeldes mit einem 'Differentialvektor'.
Beide seien nun erläutert.
Ein Vektorfeld
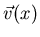 bezeichnet die Vorschrift, an jedem Raumpunkt
x einen Vektor
bezeichnet die Vorschrift, an jedem Raumpunkt
x einen Vektor 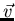 anzuheften.
In einer graphischen Darstellung hätte man dann ein hübsches
'Strömungs'-Bild.
Jeder dieser Vektoren mit seinen n Komponenten transformiert sich unter
Koordinatentransformationen wie ein normaler Ortsvektor.
anzuheften.
In einer graphischen Darstellung hätte man dann ein hübsches
'Strömungs'-Bild.
Jeder dieser Vektoren mit seinen n Komponenten transformiert sich unter
Koordinatentransformationen wie ein normaler Ortsvektor.
Die Komponenten des Differentialvektors
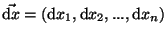 stellen die Komponentendarstellung des infinitesimalen Tangentenvektors
längs des Kurvenstücks
stellen die Komponentendarstellung des infinitesimalen Tangentenvektors
längs des Kurvenstücks
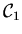 dar, das Skalarprodukt
dar, das Skalarprodukt
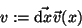 |
(21) |
ist also wieder ein Zahlenfeld für jeden Punkt aus der orientierten
Punktmenge
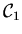 und stellt den Integranden für ein Linien-oder
Kurvenintegral dar.
und stellt den Integranden für ein Linien-oder
Kurvenintegral dar.
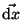 zeigt zugleich in der Richtung der Orientierung des
orientierten Kurvenstückes, es 'trägt die Orientierung von
zeigt zugleich in der Richtung der Orientierung des
orientierten Kurvenstückes, es 'trägt die Orientierung von
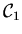 in den Integranden hinein'.
in den Integranden hinein'.
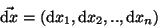 |
(22) |
Zur Erleichterung fügen wir manchmal als Index für 1-Formen die Eins an,
v1.
Die Verallgemeinerung auf mehrdimensionale orientierte Integrationsgebiete
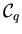 im
im
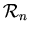 liegt dann auf der Hand:
ein physikalische Feld
wi,j,k,.. klebt an
jeden Ort des q-dimensionalen Grundgebietes im
Rnein Objekt an mit qn Komponenten.
(So hat ein Vektor in der Komponentendarstellung
einen Index, der von 1 bis n läuft). Bezüglich jedes Index transformiert
sich
wi1,i2,i3,..,iq wie ein Vektor.
Ein Beispiel ist die lokale Wirbelstärke von Strömungen von Flüssigkeiten,
bei der man an jedem Ort angeben muß wie stark die Strömung um diesen
Ort herumzuwirbeln scheint, dazu braucht man je eine Zahl für jedes
mögliche Achsenpaar der Koordinaten, also 1 für die Dimension 2,
3 für die Dimension 3, 6 für 10, usf.
oder
(n , 2) :=n(n-1)/2 für n Dimensionen. Das ist nur mit einem
Objekt wi,j mit zwei Indices unterzubringen.
liegt dann auf der Hand:
ein physikalische Feld
wi,j,k,.. klebt an
jeden Ort des q-dimensionalen Grundgebietes im
Rnein Objekt an mit qn Komponenten.
(So hat ein Vektor in der Komponentendarstellung
einen Index, der von 1 bis n läuft). Bezüglich jedes Index transformiert
sich
wi1,i2,i3,..,iq wie ein Vektor.
Ein Beispiel ist die lokale Wirbelstärke von Strömungen von Flüssigkeiten,
bei der man an jedem Ort angeben muß wie stark die Strömung um diesen
Ort herumzuwirbeln scheint, dazu braucht man je eine Zahl für jedes
mögliche Achsenpaar der Koordinaten, also 1 für die Dimension 2,
3 für die Dimension 3, 6 für 10, usf.
oder
(n , 2) :=n(n-1)/2 für n Dimensionen. Das ist nur mit einem
Objekt wi,j mit zwei Indices unterzubringen.
Entsprechend bilden wir nun für q-dimensionale Grundgebiete die
entsprechenden Produkte infinitesimaler Stücke der orientierten Fläche:
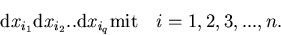 |
(23) |
Und ebenso entsprechend wird nun die q-Form wq als skalarer Integrand
eingeführt,
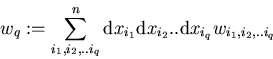 |
(24) |
Das mag für den Anfänger etwas mühsam aussehen, insbesondere doppelte
Indices ir, aber damit ist ja nur gemeint:
'nimm ein q-dimensionales orientiertes Grundgebiet, zerlege es in kleine
orientierte infinitesimale q-dimensionale
Gebiete, die das Gebiet ausschöpfen, - man
kann das Gebiet dann aus diesen infinitesimalen
Gebieten zusammenpflastern,-
spanne diese mit Hilfe der
dxir auf, und bilde dann das Skalarprodukt
mit
wi1, .. mit dem entsprechenden Index und fahre mit jedem Index
entsprechend fort.
[Die Oberfläche eines Würfels im R3 liesse
sich also mittels 'Infinitesimalen'
d xi1
d xi2pflastern, wenn nur beide Indices alle drei
Richtungen durchlaufen].
Hier ist eine historische Bemerkung angebracht:
Mathematiker benutzten den Begriff 'Infinitesimale' seit Leibniz für die
elementare Algebra des Differenzierens.
Hier dagegen sind die gleichgeschriebenen Objekte Träger der Algebra
der Differentialformen. Eine 'Algebra' ist ein konsistenter, vollständiger
Satz von Rechenregeln einer vorgelegten Klasse von Objekten.
Die 'Infinitesimale sind hier also die elementarsten Differentialformen.
Das Integral hat dann in beliebigen Dimensionen n des Raumes
über ein beliebiges orientiertes q-dimensionales Grundgebiet stets
die einfache Form des Aufsummierens der Werte der q-Form als Integrand
für jeden Punkt des Grundgebietes, fertig als Vorschrift für jede
Rechenmaschine, also auch die Vorstellung des Lesers.
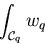 |
(25) |
Wie sichern wir uns nun dagegen, daß wir versehentlich mehr
Infinitesimale verwenden, als
 Dimensionen hat?
Wie kann denn überhaupt ein Produkt von Infinitesimalen
die Orientierung des kleinen aufgespannten Gebietes von
Dimensionen hat?
Wie kann denn überhaupt ein Produkt von Infinitesimalen
die Orientierung des kleinen aufgespannten Gebietes von
 und damit von
und damit von
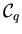 insgesamt sichern?
Dies geschieht auf einfache und anschauliche Weise durch die
Orientierungsbedingung
insgesamt sichern?
Dies geschieht auf einfache und anschauliche Weise durch die
Orientierungsbedingung
Vertauschungen von Infinitesimalen sollen durch ein Vorzeichenwechsel
geahndet werden.
Dies bewirkt automatisch, daß sich durch zwei gleiche Infinitesimale
kein Flächenstück aufspannen läßt,
|
dxi dxi = - dxi dxi = 0 .
|
(27) |
Die Orientierung der Grundgebiete einer Integration bewirken eine
Antisymmetrie der Integranden.
Alle Integranden eines Integrals im
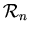 über eine
q-dimensionale orientierte Fläche bilden
einen ''antisymmetrischen Raum',
den
über eine
q-dimensionale orientierte Fläche bilden
einen ''antisymmetrischen Raum',
den
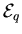 . Ersichtlich sind dessen
Eigenschaften von der Dimension n des
einbettenden Raumes
. Ersichtlich sind dessen
Eigenschaften von der Dimension n des
einbettenden Raumes
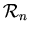 abhängig.
abhängig.
Jeder Integrand. Fq im
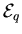 wird durch Festlegung seiner Komponenten
festgelegt. So hat ein Kurvenintegrand als
'1-Form'
wird durch Festlegung seiner Komponenten
festgelegt. So hat ein Kurvenintegrand als
'1-Form'
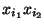 die n Komponenten des Vektors
die n Komponenten des Vektors
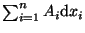 als
charakterisierende Zahlen,
bei einem Flächintegranden als '2-Form'
als
charakterisierende Zahlen,
bei einem Flächintegranden als '2-Form'
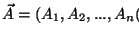 zunächst die n2 Komponenten des Tensors
Fi,j als charakterisierende Zahlen.
Wegen der Antisymmetrie
dxidxj=-dxjdxisind es jedoch nur
zunächst die n2 Komponenten des Tensors
Fi,j als charakterisierende Zahlen.
Wegen der Antisymmetrie
dxidxj=-dxjdxisind es jedoch nur
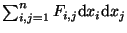 .
Interessanterweise sind diese
Fakultätenausdrücke symmetrisch:
(n q) = (n n-q).
Daher hat eine q-Form in einem
.
Interessanterweise sind diese
Fakultätenausdrücke symmetrisch:
(n q) = (n n-q).
Daher hat eine q-Form in einem
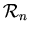 gleichviele charakterisierende Zahlen wie
eine (n-q) Form im gleichen Raum.
Die q-Formen im
gleichviele charakterisierende Zahlen wie
eine (n-q) Form im gleichen Raum.
Die q-Formen im
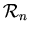 ,
die den
,
die den
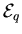 bilden, lassen sich bijektiv auf
den
bilden, lassen sich bijektiv auf
den
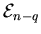 des
des
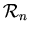 abbilden.
Diese schöne Eigenschaft der Integranden
über orientierte Punktmengen werden wir im
Folgenden nutzen.
abbilden.
Diese schöne Eigenschaft der Integranden
über orientierte Punktmengen werden wir im
Folgenden nutzen.
Die Antisymmetrie der Integranden, gebildet aus physikalischer Observabler
und Infinitesimalen über einem orientierten Grundgebiet läßt
scheinbar keinen Platz für die Vielzahl der ja bekannten unter Spiegelungen
symmetrischen physikalischen Observablen, so ändert sich weder die
Dichte von Materie in einem infinitesimalen Gebiet unter Spiegelungen,
noch die Quellstärke eines sumpfigen Gebietes, beides gut beobachtbare
Größen.
Die Präparation solcher unter Spiegelungen 'invarianter' Objekte
geschieht nun durch den großen Symmetrisator, manchmal auch einfach
Stern-Operator,  ,
genannt.
,
genannt.
Der Stern-Operator bildet jeden Integranden
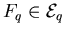 ab in einen neuen Integranden
ab in einen neuen Integranden
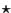 .
Der Raum aller q-Formen (q-dimensionalen Integranden) im
.
Der Raum aller q-Formen (q-dimensionalen Integranden) im
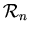 ist isomorph dem Raum aller (n-q)-Formen (n-q-dimensionalen Integranden)
im
ist isomorph dem Raum aller (n-q)-Formen (n-q-dimensionalen Integranden)
im
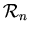 .
.
Als erstes Beispiel betrachten wir die Dichte einer vorgelegten Materieprobe,
die oft mit 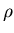 bezeichnet wird. Sie gibt zu jedem Ort eines infinitesimalen
Volumgebietes
eine Zahl, deren Mittelwert M über ein endliches Raumgebiet mit Messungen
verglichen werden kann.
bezeichnet wird. Sie gibt zu jedem Ort eines infinitesimalen
Volumgebietes
eine Zahl, deren Mittelwert M über ein endliches Raumgebiet mit Messungen
verglichen werden kann.
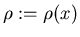 ist also eine skalare Funktion und daher als Integrand
über ein Raumgebiet
ist also eine skalare Funktion und daher als Integrand
über ein Raumgebiet 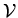 mit dem Volumen V ungeeignet.
Der große Symmetrisator rettet uns aus dieser selbstgestellten Falle.
mit dem Volumen V ungeeignet.
Der große Symmetrisator rettet uns aus dieser selbstgestellten Falle.
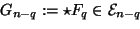 |
(28) |
für den
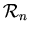 ,
-und der Leser erkennt die übliche Formel für den Fall dreier Dimensionen
,
-und der Leser erkennt die übliche Formel für den Fall dreier Dimensionen
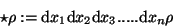 |
(29) |
M ist für kleine Raumgebiete
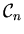 proportional zum Volumen von
proportional zum Volumen von
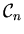 ,
,
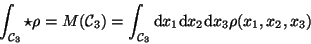 |
(30) |
mit 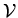 als dem Volumen des Gebietes
als dem Volumen des Gebietes
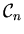 in der früher gebräuchlichen Formulierung.
Ersichtlich hat der Symmetrisator ein Objekt aus
in der früher gebräuchlichen Formulierung.
Ersichtlich hat der Symmetrisator ein Objekt aus
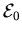 in
in
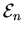 abgebildet, nämlich
abgebildet, nämlich
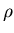 in
in
 .
Beide Integranden haben als Träger der physikalischen Information,
als 'Variable' nur die eine Zahl
.
Beide Integranden haben als Träger der physikalischen Information,
als 'Variable' nur die eine Zahl 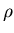 .
Information ist also durch die Abbildung nicht verloren gegangen.
.
Information ist also durch die Abbildung nicht verloren gegangen.
Diese Abbildung läßt sich nun für beliebige Dimension q des
Grundgebietes verallgemeinern. Stets bildet der Stern-Operator
einen Integranden aus
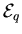 auf einen solchen aus
auf einen solchen aus
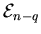 ohne Informationsverlust ab. Das wollen wir nun üben.
ohne Informationsverlust ab. Das wollen wir nun üben.
Nehmen wir ein Strömungsfeld
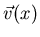 einer Flüssigkeit.
Die Strömungsgeschwindigkeiten
einer Flüssigkeit.
Die Strömungsgeschwindigkeiten 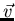 sind ein Vektorfeld,
der zugehörige Integrand eines Linienintegrals über ein
Kurvenstück ist
sind ein Vektorfeld,
der zugehörige Integrand eines Linienintegrals über ein
Kurvenstück ist
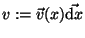
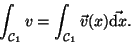 |
(31) |
Einen solchen Integrand nennt man entsprechend auch 1-Form, er ist
ein Element aus dem
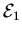 .
Es werden an jedem Ort des Pfades die Projektionen des Strömungsfeldes
längs des Weges aufsummiert.
Ersichtlich hat v im
.
Es werden an jedem Ort des Pfades die Projektionen des Strömungsfeldes
längs des Weges aufsummiert.
Ersichtlich hat v im
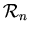 genau n unabhängige Komponenten
(charakterisierende Zahlen, die man messen
könnte) und ist eine 1-Form, seine
Komponenten vi sind ein Vektor.
genau n unabhängige Komponenten
(charakterisierende Zahlen, die man messen
könnte) und ist eine 1-Form, seine
Komponenten vi sind ein Vektor.
Aber was ist dann 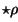 ?
Wir geben nun die allgemeine Definition des Stern-Operators und nutzen sie
dann für die gestellte Frage.
?
Wir geben nun die allgemeine Definition des Stern-Operators und nutzen sie
dann für die gestellte Frage.
Der Sternoperator schaut bei einer q-Form, also einem vorgelegten
Integranden eines Integrals über ein q-dimensionales Gebiet nach,
welche der möglichen Auswahlen von den ja zum Integrieren notwendigen
Produkten von q verschiedenen Infinitesimalen im Integranden vorhanden sind,
ersetzt diese durch jeweils genau die
übrigen n-q Infinitesimale.
Hinzu kommt ein Vorzeichen, falls die gedachte Aneinanderreihung der
Raumkomponentenindices der Infinitesimale keine gerade Permutation der
Zahlenreihe 1,2,3,4,... ist.
Das Strömungsfeld
v = v1dx1 + v2dx2+ ...+ ... +vndxnhat n unabhängige Komponenten. Der Sternoperator ist dann leicht
nach der Vorschrift anzuwenden, denn es fehlen ja jeweils alle Infinitesimale
bis auf je eins, jeder Summand erhält dann also genau die komplementären
Infinitesimale (und wir achten auf die
zyklische Reihenfolge der Indices, damit das
Vorzeichen möglichst stets positiv ist):
 |
(32) |
Ersichtlich hat der neue Integrand
 ebenfalls n Komponenten, es ist
also keine Information verloren gegangen, aber die Summanden sind jeder
ein Integrand für ein Integral über ein n-1-dimensionales
Grundgebiet.
ebenfalls n Komponenten, es ist
also keine Information verloren gegangen, aber die Summanden sind jeder
ein Integrand für ein Integral über ein n-1-dimensionales
Grundgebiet.
Beispiel:
Die Anschauung ist im
 einfach: nehmen wir einen geschlossenen
Weg
einfach: nehmen wir einen geschlossenen
Weg
 in der Ebene, so ist
in der Ebene, so ist
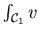 das Linienintegral
der Strömungskomponente von
das Linienintegral
der Strömungskomponente von 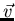 längs des Weges.
Dies ist zum Beispiel das 'Arbeitsintegral'
in der klassischen Mechanik:
längs des Weges.
Dies ist zum Beispiel das 'Arbeitsintegral'
in der klassischen Mechanik:
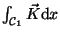 (Kräfte, für die dieses verschwindet, nennt man dann
'konservativ').
Nach dem Satz von Green-Stokes-Gauß kann man das Integral aber nun in
ein Flächenintegral umformen, denn die geschlosssene Linie ist ja Rand der
umrandeten Fläche:
(Kräfte, für die dieses verschwindet, nennt man dann
'konservativ').
Nach dem Satz von Green-Stokes-Gauß kann man das Integral aber nun in
ein Flächenintegral umformen, denn die geschlosssene Linie ist ja Rand der
umrandeten Fläche:
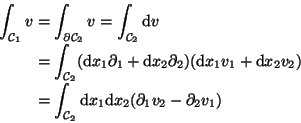 |
(33) |
Dieser Flächenintegrand ist schön antiymmetrisch, und natürlich
für beliebige orientierte Flächen im 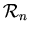 definiert mit den
n(n-1)/2 Komponenten
definiert mit den
n(n-1)/2 Komponenten
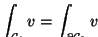 für alle
für alle
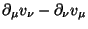 .
In drei Dimensionen gibt es für dieses Objekt gerade
3(3-1)/2=3Komponenten, und es ist historisch üblich, für diese eine Kurzschreibweise
einzuführen, die den Sternoperator ausnutzt:
.
In drei Dimensionen gibt es für dieses Objekt gerade
3(3-1)/2=3Komponenten, und es ist historisch üblich, für diese eine Kurzschreibweise
einzuführen, die den Sternoperator ausnutzt:
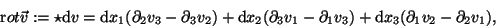 |
(34) |
die 'Rotation' von 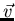 .
Zwar bilden diese drei Komponenten keinen Vektor, weil sie unter
Spiegelungen ihr Vorzeichen nicht ändern, aber das wurde sprachlich behoben,
indem man dies einen 'axialen Vektor' nannte.
Natürlich gibt es in weniger oder mehr als drei Raumdimensionen keine
Rotation, wohl aber stets die Objekte
.
Zwar bilden diese drei Komponenten keinen Vektor, weil sie unter
Spiegelungen ihr Vorzeichen nicht ändern, aber das wurde sprachlich behoben,
indem man dies einen 'axialen Vektor' nannte.
Natürlich gibt es in weniger oder mehr als drei Raumdimensionen keine
Rotation, wohl aber stets die Objekte
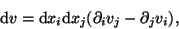 |
(35) |
das totale Differential von v.
23
Dagegen hat das Integral über
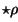 einen
ganz anderen Wert und Bedeutung:
einen
ganz anderen Wert und Bedeutung:
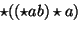 |
(36) |
Nehmen wir eine einfache geschlossene Kurve:
das Rechteck, gebildet aus den Linien in der
x,y-Ebene: von (-1,-1) zu (1,-1) zu (1,1) zu
(-1,1) und zurück zu (-1,-1).
Das Vektorfeld sei
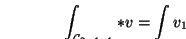 .
Beide Komponenten von
.
Beide Komponenten von 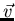 haben also an jedem Raumpunkt (x,y) einen
Wert. In diesem Beispiel nehmen wir an, es
sei speziell
haben also an jedem Raumpunkt (x,y) einen
Wert. In diesem Beispiel nehmen wir an, es
sei speziell
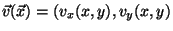 .
Dann stömt es schön an allen Randpunkten
von innen nach außen, radial vom
Ursprung weg.
Das o.g. Integral wird dann einfach
.
Dann stömt es schön an allen Randpunkten
von innen nach außen, radial vom
Ursprung weg.
Das o.g. Integral wird dann einfach
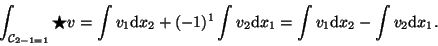 |
(37) |
und die Auswertung ergibt
-(-1) 2 + 1 2 + 1 2 -(-1) 2 = 8,
überall am Rande strömt es heraus aus dem Karton.
Physikalisch summiert das Integral über den ganzen Rand, was
herausströmt.
Zugleich ist aber das Rechteck die orientierte Randkurve zur
Rechteckfläche:
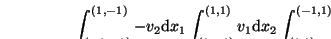 ,
der umrandeten Rechteckfläche und das Randintegral wird nach
dem Satz von Green-Stokes-Gauss zu einem Flächenintegral über
das Differential des Randintegral-Integranden,
,
der umrandeten Rechteckfläche und das Randintegral wird nach
dem Satz von Green-Stokes-Gauss zu einem Flächenintegral über
das Differential des Randintegral-Integranden,
Dieser schöne symmetrische Integrand heißt in der älteren
Literatur auch
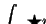 oder Divergenz
des Vektorfeldes
oder Divergenz
des Vektorfeldes
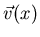 .
Es mißt die lokale Quellstärke. Das Integral summiert
diese dann über alle Quellpunkte im Rechteck zur integralen
Gesamtquellenstärke des Rechteckes, was man makroskopisch messen kann.
.
Es mißt die lokale Quellstärke. Das Integral summiert
diese dann über alle Quellpunkte im Rechteck zur integralen
Gesamtquellenstärke des Rechteckes, was man makroskopisch messen kann.
XXXXXXXXXhier wird gearbeitetZXXXXXXXXXXXXX
Längs des Wegstückes
dx2 wird der Wert der Komponente von 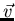 senkrecht dazu (in 1-Richtung) aufsummiert, und beim zweiten Summanden ist es
analog.24
Das Vorzeichen sorgt nun dafür, daß auf allen vier Integrationsstücken
stets die Komponente von
senkrecht dazu (in 1-Richtung) aufsummiert, und beim zweiten Summanden ist es
analog.24
Das Vorzeichen sorgt nun dafür, daß auf allen vier Integrationsstücken
stets die Komponente von 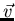 gemessen und aufsummiert wird,
die senkrecht zur Integrationskurve und aus dem Volumstück heraus strömt.
Insgesamt mißt also
gemessen und aufsummiert wird,
die senkrecht zur Integrationskurve und aus dem Volumstück heraus strömt.
Insgesamt mißt also 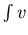 die Zirkulation von v um das
Flächenstück
die Zirkulation von v um das
Flächenstück
 und
und
 die gesamte Quellstärke
(Die Menge an Flüssigkeit, die aus dem Rand insgesamt herausströmt,
denkt man sich im Innern durch eine Quelle eingebracht..).
Da an jedem Kurvenpunkt der Geschwindigkeitsvektor zwei Komponenten hat
(wir haben ja ein ebenes Problem), sind damit alle 'Freiheitsgrade'
von
die gesamte Quellstärke
(Die Menge an Flüssigkeit, die aus dem Rand insgesamt herausströmt,
denkt man sich im Innern durch eine Quelle eingebracht..).
Da an jedem Kurvenpunkt der Geschwindigkeitsvektor zwei Komponenten hat
(wir haben ja ein ebenes Problem), sind damit alle 'Freiheitsgrade'
von 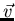 abgebildet auf entsprechend
viele unabhängige Integrale
und damit meßbare Observable.
abgebildet auf entsprechend
viele unabhängige Integrale
und damit meßbare Observable.
In höheren Dimensionen für das Grundgebiet und den Raum wird
zunehmend die Anschauung strapaziert, - und der Rechner ohne Kenntnis der
Regeln für Integranden verliert leicht die Kontrolle über die Vorzeichen.
Aber vor beidem schützt der große Vorteil der Formulierung mit
Integranden: die Formeln gelten in gleicher Form für alle
Werte von q und n.
Nehmen wir den Drehimpuls als ein Beispiel:
Er hat so viele unabhängige Komponenten (meßbare Zahlen,wie
es Möglichkeiten gibt, zwei Koordinatenachsen aus den gegebenen nauszuwählen, nennen wir sie i und j,
die entsprechenden Kompenenten des Impulses und des Ortsvektors zu messen und
als Variable die Differenz
xipj - yi zu bilden.
Ersichtlich gibt es
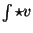 solche Paare25, also in zwei Dimensionen
eine, in drei Dimensionen drei, in vier Dimensionen sechs, und so fort.
solche Paare25, also in zwei Dimensionen
eine, in drei Dimensionen drei, in vier Dimensionen sechs, und so fort.
Alle Komponenten des Drehimpulses bilden zusammen einen
antisymmetrischen Tensor, denn seine Komponenten ändern bei Vertauschung
zweier Indices das Vorzeichen und die Diagonalelemente sind ersichtlich Null
(gleiche Indices).
Man nennt ein solches Objekt nicht Matrix sondern Tensor, weil sich
die Komponenten dieser Matrix unter Koordinatentransformationen wie ein
Vektor bezüglich jedes der beiden Indices verhält.
Welche Integrationen können wir nun sinnvoll mit diesem Objekt ausführen.
Dazu bilden wir zunächst aus dem Orts- und Impulsvektor die entsprechenden
1-Formen und multiplizieren diese mit dem Ergebnis der 2-Form 'Drehimpuls'
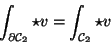 |
(41) |
Gemäß einer von Einstein beim Segeln auf dem Schilf-umrandeten
Kaput-See bei Berlin ersonnenen und nach ihm benannten
Einstein-Konvention kann man in Formeln
in der Physik, in denen Summen über Koordinatenindices
auftauchen, das Summenzeichen stets
beim Schreiben weglassen, weil in Ausdrücken,
über die zu summieren ist, stets die entsprechenden
Indices doppelt auftauchen ('Skalarproduktbildung').
Der Integrand Drehimpuls l hat zwei Infinitesimale, ist also ein
Integrand über eine Fläche.
Als sinnvoll meßbare Größe erhalten wir damit den Gesamtdrehimpuls
der Teilchen oder der Strömung, die an jedem Ort der Fläche einen
Impuls (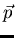 bzw.
bzw.
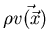 besitze (der auch Null sein kann). Durch den Flächeninhalt geteilt, ergäbe sich
eine Drehimpulsdichte.
besitze (der auch Null sein kann). Durch den Flächeninhalt geteilt, ergäbe sich
eine Drehimpulsdichte.
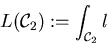 |
(42) |
So einfach wird dies durch die Nutzung der Integranden.
Und von der Dimension des Raumes
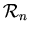 ,
in dem diese Fläche liegt,
ist die Formel, da mit Integranden geschrieben, vollkommen unabhängig.
,
in dem diese Fläche liegt,
ist die Formel, da mit Integranden geschrieben, vollkommen unabhängig.
Wir können nun aber aus l noch einen weiteren Integranden erzeugen,
indem wir den Stern-Operator anwenden, den 'großen Symmetrisator'.
![\begin{displaymath}\star l =
\epsilon(i,j;[1,2,3,..,n;/i,j]) \left[ {\mathrm d}x...
... {\mathrm d}x_{n}
/ {\mathrm d}x_{i} {\mathrm d}x_{j} \right]
\end{displaymath}](img131.gif) |
(43) |
Das sieht etwas mühsam aus, ist ja auch in n Raumdimensionen.
Das 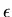 besagt aber einfach, daß ein Vorzeichen hinzugefügt werden
soll, wenn die Zahlenfolge
i,j;[1,2,3,..n;/i,j] also die Zahlen in der
Reihenfolge i, j und dann von 1 anfangend bis n aber unter Auslassung
der ja bereits vorhandenen i,j bis n.
besagt aber einfach, daß ein Vorzeichen hinzugefügt werden
soll, wenn die Zahlenfolge
i,j;[1,2,3,..n;/i,j] also die Zahlen in der
Reihenfolge i, j und dann von 1 anfangend bis n aber unter Auslassung
der ja bereits vorhandenen i,j bis n.
Nun wollen wir das 'totale' Differential einer
Form kennenlernen. Das ist nichts anderes als
die Verallgemeinerung der gewöhnlichen
Ableitung auf Formen statt Funktionen und
auf beliebig viele Dimensionen. Um den Leser
nicht zu verschrecken: der Formalismus soll
wieder dimensionsunabhängig
und koordinatenfrei formuliert werden. Noch besser:
viele der verwirrend vielen und kompliziert zu
nutzenden Operationen wie 'Divergenz', 'Gradient',
'Rotation', die in verschiedenen Dimensionen ganz
verschieden zu handhaben sind,
werden wir nur ein einziges mathematisches Objekt
benötigen: das totale Differential mit der
Notation, - wie könnte es anders sein:
d .
Wieder beginnen wir mit einigen Beispielen:
Eine gewöhnliche Funktion einer Variablen, F(x)
ergebe abgeleitet
die neue Funktion einer Variablen
f(x) := F'(x).
Als Notation für die Ableitung nach x werden oft auch
andere Notationen verwandt:
|
F'(x) = d F/x = d /d x F = d x F = ...
|
(44) |
Wir verzichten wieder auf alle wunderbaren Erweiterungen, die
sich erst in gekrümmten vieldimensionalen Räumen
erschließen.
Das bisher verwendete 'Infinitesimal'
d x erweist sich nun
als Differential der Koordinate x,
d x =d x(Tautologien sind ja auch was Schönes).
Dieses Dokument soll auch eine Hilfe geben für die Probleme der
Nutzung, Akzeptanz neuer Darstellungen physikalischer Inhalte mittels
mathematischer Objekte und damit verbunden anderer Schreibweisen in der Physik.
Die Studenten der Physik des zweiten Semesters in Oldenburg haben daher
zu einer Serie von 'Streitgesprächen', genauer aber von
'Teamteaching' zur Darstellung der Physik in der
Lehre in den Anfangssemestern' eingeladen. Hierauf sind wir gespannt.
Die Themen aus unserer Sicht sind im
Anhang 'Streitgespräche'
aufgeführt.
Eine erste Runde fand zum Thema Der Spin und seine Darstellung in den
ersten Semestern im SS 1999 statt.
Physiker aller Semester, besonders aber Anfangssemester laden wir zu
einem Fußballspiel ein.
Der erste Torschütze bekommt eine gute Flasche Rotwein.
Weitere Torschützen kommen in die 'Hall of Fame'.
Die Regeln finden sich im
Anhang 'Fussballspiel'.
Sie sind noch in einem frühen
Zustand.
Studenten der Generation (1. Semester: WS.1997) haben interessante
Links aus dem Internet zusammengetragen und nach Themen
geordnet, die
Workbench Theoretische Physik.
Vorlesungsskript zur Analysis I und II
H. Wolter
Lehrmaterial anderer Autoren zur Einführung der Theoretischen Physik
Transcript of algebra used in an introductory physics text
Im Internet finden wir ein Skript von W. Lücke, Univ. Clausthal.
Einführung in die Theoretische Physik.
Wir emfehlen dies als vertiefende Lektüre.
As an example of the usefulness of the differential forms notation
we transcribe K. Hinsch, Concepts of Physics (Grundlagen physikalischer
Messungen (Grundkurs Physik I)), Kapitel 7
'General characterization of fields'.
For guidance we set the section numbers to the same values as the script
and it is recommended to have this on the desk 26
and even use the same page numbers, - to ease the demonstration how much
the use of integrands shorten and simplify and thus make physics more
easily understandable. - But the text is written such that you may read
it without the experimental textbook at hand as well.
27
Remember that all formulae given here work in any dimension
and curved space not just the Euklidean
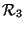 as used here.
For a more detailed, and even more elementary introduction to differential forms,
see the main part of these lectures.
as used here.
For a more detailed, and even more elementary introduction to differential forms,
see the main part of these lectures.
Basic ingredients are the total
derivative d, the star operator
 ,
amd the oriented
point-manifolds
,
amd the oriented
point-manifolds
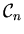 in ndimensions.
in ndimensions.
The total derivative is defined by
| |
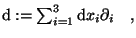 |
|
(45) |
| |
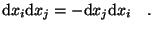 |
|
(46) |
The  operator picks all
dxk found in an expression, and replaces them by all
dxl not found, multiplied by an eventual sign, if the ordered list of
all k and then l is not an even
permutation of 1..3, with n=3, the dimension of the
space. Thus in
operator picks all
dxk found in an expression, and replaces them by all
dxl not found, multiplied by an eventual sign, if the ordered list of
all k and then l is not an even
permutation of 1..3, with n=3, the dimension of the
space. Thus in
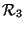 we have simply
we have simply
 ,
and
,
and
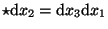 ,
and
dx1dx2=dx3, and so forth.
,
and
dx1dx2=dx3, and so forth.
Check
 apart from an eventual minus sign, and
d d =0.
apart from an eventual minus sign, and
d d =0.
For any curve, sheet, or volume area,
respectively we write
 respectively.
In Physics only oriented point
manifolds
respectively.
In Physics only oriented point
manifolds
 occur.
For their surfaces we write
occur.
For their surfaces we write
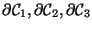 ,
respectively, which
are just: the two endpoints of the
given curve, the borderline of the twodimensional sheet, and the
surface of the volume area,
respectively. It may be unusual to you
to read the endpoints of a curve as 'the oriented set of points of the
border of the curve', but thats what it is and reminds you neatly for the
minus sign in case of an integral,
,
respectively, which
are just: the two endpoints of the
given curve, the borderline of the twodimensional sheet, and the
surface of the volume area,
respectively. It may be unusual to you
to read the endpoints of a curve as 'the oriented set of points of the
border of the curve', but thats what it is and reminds you neatly for the
minus sign in case of an integral,
![$\int_a^b \mathrm d x f'(x)= \int_{{\cal C}_{{1[a,b]}}}
f(b)-f(a)=\int_{{\cal C}_{{0}}} f $](img141.gif) .
We use the integrands now
throughout whenever no argument of a function is given.
.
We use the integrands now
throughout whenever no argument of a function is given.
Check
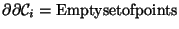 for any i=1,2,3. This is called the lemma of Columbus since
he had to rely on it when sailing West to find America, that there
is no rim of the earth's surface
anywhere between.
for any i=1,2,3. This is called the lemma of Columbus since
he had to rely on it when sailing West to find America, that there
is no rim of the earth's surface
anywhere between.
Scalars of the types
| |
A := A(x1,x2,x3) |
|
(47) |
| |
B := B1(x1,x2,x3)dx1
+ B2(x1,x2,x3)dx2
+ B3(x1,x2,x3)dx3 |
|
(48) |
| |
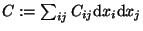 |
|
(49) |
| |
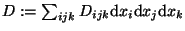 |
|
(50) |
these socalled
(0,1,2,3), respectively, Forms are scalars and
are found as integrands of 0,1,2,3-dimensional integrals.
Instead of infinitesimals multiplied by a function summed over infinitesimal
pieces of the integration space region now the calculation of an integral is
easy: take every point of any given space object
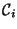 ,
calculate the
numerical value of the scalar
integrand for that point and add them.
Given a flow velocity field,
(imagine the velocity field of flowing
water,
with the vector of velocity attached to
each point in space),
which is a 1-form
,
calculate the
numerical value of the scalar
integrand for that point and add them.
Given a flow velocity field,
(imagine the velocity field of flowing
water,
with the vector of velocity attached to
each point in space),
which is a 1-form
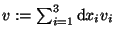 .
What is the amount of 'water' flowing out through a given
closed surface area
.
What is the amount of 'water' flowing out through a given
closed surface area
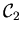 separating the interior
volume area
separating the interior
volume area
 with
with
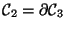 .
Closed surface means just
.
Closed surface means just
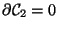 in this case. Think of a sphere
in this case. Think of a sphere
 ,
its surface
,
its surface
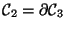 ., and its empty set of points
., and its empty set of points
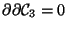 .
.
We do not need to define or use orientation vectors
'pointing vertical' outwards of the surface. This would not
work e.g. for the same example but in one dimension less.
The total flux out of
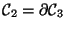 is to be defined as
is to be defined as
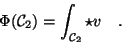 |
(51) |
Assume no sinks inside the volume. This
would mean
the divergence
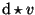 to be zero everywhere inside.
The continuity condition thus
demands that what flowed in through
to be zero everywhere inside.
The continuity condition thus
demands that what flowed in through
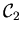 has to flow out
at some other part of the surface.
has to flow out
at some other part of the surface.
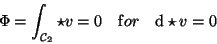 |
(52) |
This reasonable claim follows from
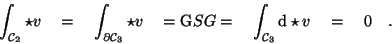 |
(53) |
'GSG' stands for the one relation named
at different occasions after Green, Stokes, Gauß and
so many other authors.
Thus 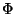 measures the 'total source strength' of all
sources inside the volume area
measures the 'total source strength' of all
sources inside the volume area
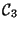 .
It is
a 0-Form or a'number'
(that is for water: the amount in liter per second, being
created inside and flowing out, etc.).
If all local sources are just some point sources
('dwells'), then
.
It is
a 0-Form or a'number'
(that is for water: the amount in liter per second, being
created inside and flowing out, etc.).
If all local sources are just some point sources
('dwells'), then
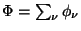 .
.
The advantage of the usage of integrands is thus:
- no introduction of orthogonal vectors on
surface pieces pointing into an outer space which might
not exist, is necessary,
- no explicit calculation for simple cases
necessary for proof,
- Orientation is built in automatically,
- simply generalizable for any higher (or lower)
dimensions, and curved spaces,
- less to learn and write.
Example: Does the electric field have sources?
In Electromagnetism the force on an electric test
charge divided by its charge is
called the electric field thrength E.
As a force field it is a 1-Form,
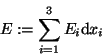 |
(54) |
where the Ei are the components of the
electric field strength vector for each
point xi.
Its divergence is called 'local charge density'
and its volume integral total charge Q.
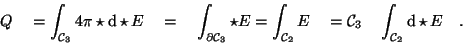 |
(55) |
28
Check
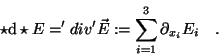 |
(56) |
That is why the star operation is called sometimes
mystically 'the great symmetrizer'.
For the relation between electric charges, say
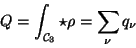 |
(57) |
and by making use of
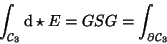 |
(58) |
we gain the wellknown relation between the charge
and
the electric field strength distribution,
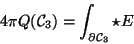 |
(59) |
in integral form or equivalently
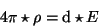 |
(60) |
in differential form, known as Gauß-law
29.
Of course we use the usual [cgs] system for
dimensions30
As a comment:
Sometimes an unmeasurable field, called 'potential' is
introduced to 'elucidate' Gauß law.
We give two possibilities (out of many).
1.) E being 'conservative force', it may be represented in
terms of a new 0-Form, the 'potential' V with
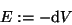 |
(61) |
Inserting this we get
(the components of which are of course those of
'
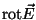 '
in differential form or, since
d E
is a 2-Form, the
equivalent integral formulation for any (not necessarily
closed) twodimensional sheet of points
'
in differential form or, since
d E
is a 2-Form, the
equivalent integral formulation for any (not necessarily
closed) twodimensional sheet of points
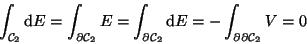 |
(63) |
with no actual calculatin necessary, since we know that
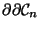 for any manifolds in any dimension.
The existence of such an integrability is named as
Maxwell-equation for electrostatic fields.
for any manifolds in any dimension.
The existence of such an integrability is named as
Maxwell-equation for electrostatic fields.
One of the equivalent formulations is:
Assume the existence of a 0 form field W to construct
a 1-form, sometimes called 'vectorpotential'
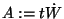 with t being the time.
Then represent the electric field
by
with t being the time.
Then represent the electric field
by
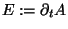 and the result is the same.
and the result is the same.
The suitable choice of a potential field to describe
the Maxwell-euation is called 'gauge', since it can be
tuned or gauged to some extent by choice, here either
by a choosing a 0-form V or a 1-form A.
The latter is called the 'preferred gauge' for reasons to
become exhibited as late as when we discuss the
relativistic quantum electrodynamics where it allows
to use the Hamilton formalism in contrast to the choice of
V which sticks with the Lagrangian formalism.
In engeneering and meteorology as well as airplane construction a
macroscopic formualation is preferred, using the Circulation Z
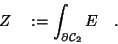 |
(64) |
For conservative fields (that is E= -dV) the circulation vanishes,
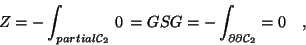 |
(65) |
which just uses the result that for any n always
 .
Alternatively we could have used the GSG to calculate Z by
.
Alternatively we could have used the GSG to calculate Z by
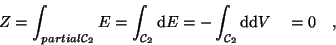 |
(66) |
since
d d =0 in any dimension space.
Fields with Z=0 are sometimes called irrotational, since
there is no net flux along a closed loop.
We now consider two examples: the rotation of flow fields as found in
nature in meteorological depressions, (tangential velocities proportional
to the distance from the center) and the cirulationless whirls such as
the meteorological taifuns (tangential velocities proportional to
the inverse of the distance to the centre).
Example: Velocity in the rotation of a 'solid body'
 |
(67) |
if consequently read from right to left: calculate the components of
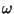 ,
apply the star-operator to it, take the (exterior) product with
r, that is just multiply with
,
apply the star-operator to it, take the (exterior) product with
r, that is just multiply with
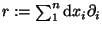 from the left to it and finally again apply the star-operator.
from the left to it and finally again apply the star-operator.
Why this ansatz for v ?
We have to get an understanding of rotation of, say a piece of twodimensional
plate taking one point fixed, insert in the plane the plate is defining
a coordinate system, say i,j and then turn the plate by a given angle
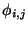 by grabbing the axis i and turning it into the direction of
j. If the plate happens to be embedded in a n-dimensional space, -no
problem: just keep all other axes, with the execption of the involved two,
i,j, fixed. Thus we see, that rotation is defined not by a 'rotation
axis', but by the two axes defining the rotation plane and the turning
angle. This definition works in any dimensional space.
In case, we did not take the correct angles, do not worry: just take the
two form rotation of i into j by the angle
by grabbing the axis i and turning it into the direction of
j. If the plate happens to be embedded in a n-dimensional space, -no
problem: just keep all other axes, with the execption of the involved two,
i,j, fixed. Thus we see, that rotation is defined not by a 'rotation
axis', but by the two axes defining the rotation plane and the turning
angle. This definition works in any dimensional space.
In case, we did not take the correct angles, do not worry: just take the
two form rotation of i into j by the angle
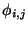 summing over all possibilities. The time derivative of it is the
angular velocity
summing over all possibilities. The time derivative of it is the
angular velocity 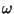 ,
,
 |
(68) |
to be summed over all indices that occur twice, that is i,j.
As an example let us take a twodimensional plane, and turn axis 1 into
2 by the single angle  .
Then
.
Then  just has the one component
just has the one component
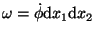 and thus simply
and thus simply
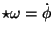 ,
or a 0-form.
Now multiply
,
or a 0-form.
Now multiply
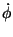 by the 1-form
r:= x1 dx1 + x2 dx2and again apply the star-operator to arrive at
by the 1-form
r:= x1 dx1 + x2 dx2and again apply the star-operator to arrive at
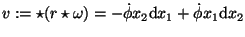 and that are just the components of the velocity of a rigidly
rotating plane around the center with the angular speed
and that are just the components of the velocity of a rigidly
rotating plane around the center with the angular speed
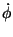 .
So e.g. a point on the 1-axis (that is with coordinates (x1, 0)inserted moves upwards, as it should:
.
So e.g. a point on the 1-axis (that is with coordinates (x1, 0)inserted moves upwards, as it should:
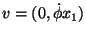 and thus just proportional to the distance from
the center. Such a velocity distribution is known from (hopefully) rigid
rotation of a carousel or from the wind speeds and direction around an
ordinary meteorological depression, the wind speed increases with the
distance from the centre.
and thus just proportional to the distance from
the center. Such a velocity distribution is known from (hopefully) rigid
rotation of a carousel or from the wind speeds and direction around an
ordinary meteorological depression, the wind speed increases with the
distance from the centre.
One of the advantages is now, that v as a 1-form is an integrand and
can thus readily be integrated along any one-dimensional curve,
 .
For a closed curve, that is thus the boundary or an
area
.
For a closed curve, that is thus the boundary or an
area
 and a time-constant speed of rotation
and a time-constant speed of rotation
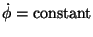 this gives
this gives
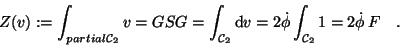 |
(69) |
because
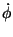 is assumed a constant; The object 1 in the last integral
is of course the elementary one-form
dx1dx2 .
The integration was simple, just remember
is assumed a constant; The object 1 in the last integral
is of course the elementary one-form
dx1dx2 .
The integration was simple, just remember
 and multiply this with the components
of the above given v.
and multiply this with the components
of the above given v.
F is the area of the part of the plane which is enclosed by the
closed curve
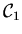 we started of with.
Hope, the reader enjoys that we do not have had to actually calulate
anything specific nor retreat to just circles.
we started of with.
Hope, the reader enjoys that we do not have had to actually calulate
anything specific nor retreat to just circles.
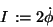 |
(70) |
is called the vorticity or 'circulation per enclosed area.
Be a vector field 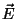 be given with its components
(here for two dimensions of the space)
be given with its components
(here for two dimensions of the space)
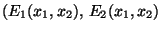 .
It defines the one-form
.
It defines the one-form
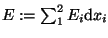 .
For higher dimensions of the space just add the respectice components.
.
For higher dimensions of the space just add the respectice components.
There are two differential operations we can perform with it:
(Check by inserting the definitions of  ,
d and E for,
say, two dimensions.
,
d and E for,
say, two dimensions.
The components of
d E are sometimes called curl E
and are the components of a twodimensional antisymmetric tensor with
no components inone dimension, one in two dimensions, and so forth.
Just in 3 dimensions we have three components.
In n dimensions we have n(n-1)) components.
Clearly
d E can be calculated in any dimension of space, but for
less than 2 it is zero.
d E is of course a 2-form.
The integration of the integrand E gives
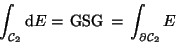 |
(73) |
a line integral over a closed line.
 is, since E is a one-form, a
is, since E is a one-form, a
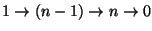 form.
The expression
form.
The expression
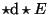 is sometimes called
div E.
is sometimes called
div E.
Physics relations are often formulated using the objects
curl and div applied to vector fields.
In addition for scalar fields, say,
V:=V(x-1,x2,..)For these
 is always zero, because of
dxi dxj=-dxj dxi. But
is always zero, because of
dxi dxj=-dxj dxi. But
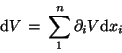 |
(74) |
is a useful one-form, the coefficients of which are the components
of the vector field
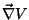 ,
sometimes called grad V.
Clearly, due to using the forms, the
,
sometimes called grad V.
Clearly, due to using the forms, the  and the dtot operators,
we gain absolute control over differential properties of physical fields
for any dimensions and any complexity of the physical objects, let they be
scalar, vector, or tensor fields.
and the dtot operators,
we gain absolute control over differential properties of physical fields
for any dimensions and any complexity of the physical objects, let they be
scalar, vector, or tensor fields.
To give some examples:
If a vector field, say the electric field strength E can be calculated
from a scalar potential field V by differentiation,
E=d V then
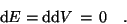 |
(75) |
because of the antisymmetry of the differentials.
The field E is then called 'rotation-free' or 'conservative'.
Of course
d d is always zero, sometimes called
'
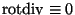 ' or
' or
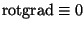 in three dimensions, beware,
but
d d Q is always zero independent of the type of the form,
- just should be a m<(n-2)form.
in three dimensions, beware,
but
d d Q is always zero independent of the type of the form,
- just should be a m<(n-2)form.
For three dimensions, some thumb rules to be able to read old
textbooks of the last century are given here
Some physical objects are listed here:
Scalar fields are mechanical potential fields
V(x1,x-2,..).
One-forms are the space point fields x, the velocity fields of a
flow, v, the momentum distribution p, the force field K,
the electric field E, and so forth.
Two-forms are e.g. the magnetic field
B:=d A with the
magnetic potential one-form A, the stress field of solids,
the angular momentum density, and so forth.
Newton's law reads
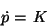 |
(79) |
.
Experiments are done by measuring.
Measured are numbers. Thus the usual vector-algebra is neither
a direct way to calculate from theory results which can be compared
with experiment. The only arguments for using operations such as
the 'vector product', the 'axial vectors' are that it works
in three dimensions, and that tradition since 50 years found its
way into textbooks, - and apparently the brains and 'Anschauung'
of the everyday physicist.
However, improving the tools in applying theory to everyday
physics has in the past resulted in major steps of getting better
'Anschauung', more direct ways to results and to application in a
wider range of fields.
Imagine, I was grown up in physics
before the usual vector algebra got into use, that is, we had to
write down and learn every single application of vector algebra with
components-writing.. E.g. calculating the vector product of two
vectors
 by the determinant
by the determinant
 |
(80) |
the result claimed to be a 'polar vector' (one which does not change
sign with mirroring).
However: What will the reader do in the case of only two dimensions
(or any other than three)
with this construction? There is no such thing as a 'polar vector'.
Instead, we construct out of the ordinary vectors
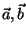 the respective integrands, as they would occur in line integrals,
if they were the basic ingredients of vector fields with constant
coefficients,
the respective integrands, as they would occur in line integrals,
if they were the basic ingredients of vector fields with constant
coefficients,
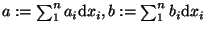 .
Thus we can apply all formulae for vector fields, and immediately
find the correct expression for the vector product, here called
the 'exterior product':
.
Thus we can apply all formulae for vector fields, and immediately
find the correct expression for the vector product, here called
the 'exterior product':
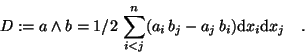 |
(81) |
The components of this two form is the antisymmetric tensor of
rank two which is the 'vector product'.
D is an ordinary two-form.
Indeed, it gives the right result not only in two but in
any dimension. And as a bridge to the past,
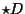 in three dimensions is indeed the historic vector-product
and a real and ordinary one-form.
in three dimensions is indeed the historic vector-product
and a real and ordinary one-form.
And the forms are scalar integrands (numbers), independent of
coordinate transformations and ready to be used to integrate
over the respective point manifolds.
Thus they are the right objects to be dealt with if one
wants to strengthen the contact to daily experimental physics.
By this first inspection we are encouraged to use the
forms formalism throughout even for the simple cases of one point
moving in space and asking for its path and its properties.
We will make use of the formalism also to calculate any of the
complicated formulae in vector calculus without
having ever to resort to the vectors, to vector products,
and the like,-- and we will thus not only have much simpler
formulae, less work and less tedious derivations, but the results
will contain all necessary signs and will work in any dimension,
including the simple twodimensional cases.
We will not need 'artifical dimensions', such as the third direction
of a 'vector product' but stay in the two dimensions spanned by
the two involved vectors.
Imagine you would meet an ant on a carousel, and explain to her,
the force dragging her to the rim needs a third dimension to be
calculated, and with this you point to the sky..
.....................................
Einführung in die theoretische Physik
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 2 einf.tex.
The translation was initiated by Eberhard Hilf on 2000-03-01



Eberhard Hilf
2000-03-01
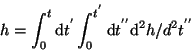
 zu.
Dabei ist
i=1,2,3,4.. ein Laufindex, der diese
Zustände der Reihe
nach abzählt. Sie sind sicher abzählbar, da sie der Experimentator
nur der Reihe nach realisieren kann. Dabei numeriert er seine Versuche durch,
und mag sie danach dann nach der Größe der Zahlen ordnen.
Sie bleiben aber abzählbar.
zu.
Dabei ist
i=1,2,3,4.. ein Laufindex, der diese
Zustände der Reihe
nach abzählt. Sie sind sicher abzählbar, da sie der Experimentator
nur der Reihe nach realisieren kann. Dabei numeriert er seine Versuche durch,
und mag sie danach dann nach der Größe der Zahlen ordnen.
Sie bleiben aber abzählbar.