Baustein 7.2: Die Ionisierungsenergie
Material
Hier findest du das Material für diese Station.
Baustein 7.2: Die Ionisierungsenergie
In Baustein 3 konntest du erfahren, dass die Elektronen Bausteine der Atome sind. Sie tragen die negative Ladung und können relativ leicht bewegt werden. Heute wissen wir, dass der Kern eines Atoms positiv geladen ist und sich die Elektronen in der Atomhülle befinden. Der Kern und die Elektronen ziehen sich also gegenseitig an, weil sie unterschiedlich geladen sind.
Beispiel: Das Wasserstoffatom
Wasserstoff ist das einfachste Element. Wasserstoff-Atome haben ein positiv geladenes Proton im Kern, welches das eine negativ geladene Elektron in der Atomhülle anzieht. Insgesamt ist ein Wasserstoff-Atom neutral.
Dieses Elektron befindet sich in einem bestimmten Abstand zum Kern. Wir können es mit einem Stein vergleichen, der auf dem Boden liegt. Wir können diesen Stein anheben. Dafür muss aber Energie zugeführt werden. Je mehr Energie wir zuführen, desto höher können wir den Stein heben.
Ähnliches gilt auch für Elektronen. Wir können ihnen Energie zuführen und damit die "Höhe", den Abstand vom Atomkern vergrößern. Einen Stein kannst du so hoch heben wie du möchtest, wenn du genügend Energie zuführst. Er kann jede Höhe, jeden Energiezustand einnehmen.
Wenn genügend Energie genutzt wird, können Elektronen sogar aus den Atomen entfernt werden. Heute können Wissenschaftler die Energie, die benötigt wird, um ein Elektron aus einem Atom zu entfernen, sehr genau messen.
Die Energie, die benötigt wird, um ein Elektron von der Anziehungskraft des positiv geladenen Kerns zu lösen, nennen wir Ionisierungsenergie.
Ionisierungsenergien der Elemente
In der folgenden Tabelle ist aufgelistet, wie viel Energie mindestens notwendig ist, um einem Atom eines Elements genau ein Elektron zu entziehen. Diese 1. Ionisierungsenergie ist für die ersten 20 Elemente dargestellt.
Hinweis: Die Einheit Elektronvolt [eV] ist die „handliche“ Einheit der Energie, wenn es darum geht sehr kleine Energiebeträge anzugeben. 1 eV sind 1,602 · 10-19 J · s. Das ist sehr wenig Energie. Wenn du 1 g Wasser um 1 Grad erwärmen möchtest, bräuchtest du dafür die Energie 2,609 · 1019 eV.
| Element | Ionisierungsenergie in eV |
|---|---|
| Wasserstoff | 13,6 |
| Helium | 24,6 |
| Lithium | 5,4 |
| Beryllium | 9,3 |
| Bor | 8,3 |
| Kohlenstoff | 11,3 |
| Stickstoff | 14,5 |
| Sauerstoff | 13,6 |
| Fluor | 17,4 |
| Neon | 21,6 |
| Natrium | 5,1 |
| Magnesium | 7,6 |
| Aluminium | 6,0 |
| Silicium | 8,2 |
| Phosphor | 10,5 |
| Schwefel | 10,4 |
| Chlor | 13,0 |
| Argon | 15,8 |
| Kalium | 4,3 |
| Calcium | 6,1 |
| ... |
Aufgabe 7.2.1 - für Profis (optional)
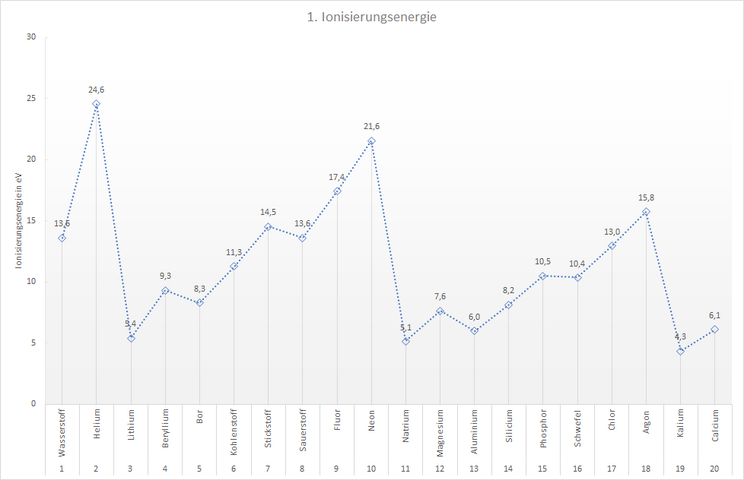
Zeichne per Hand oder mithilfe von beispielsweise Excel ein Diagramm, welches den Verlauf der Ionisierungsenergie der ersten 20 Elemente zeigt.
Verlauf der Ionisierungsenergie im Periodensystem
Mit Hilfe der Tabelle lässt sich die 1. Ionisierungsenergie der Elemente von Wasserstoff bis Calcium grafisch darstellen, man erhält das folgende Diagramm.
Aufgabe 7.2.2
- Für Profis (optinal): Formuliere schriftlich eine Beschreibung des Diagramms.
- Tipp: Das Arbeitsblatt "Strategie zur Beschreibung eines Diagramms" kann dir dabei helfen.
- Achte darauf, dass du nur beschreibst und nicht auswertest.
- Wenn du nicht die Aufgabe für Profis machst, löse die digitale Aufgabe (siehe unten). Wenn du die Lücken im Text mit den richtigen Wörtern füllst, erhältst du eine Beschreibung des Diagramms
- Ermittle anhand des Diagramms Regeln, die den groben Verlauf der Ionisierungsenergie innerhalb des Periodensystems beschreiben (wenn du Unterstützung brauchst, nutze den Tipp unten):
- Von oben nach unten (Innerhalb einer Hauptgruppe)...
- Von links nach rechts (Innerhalb einer Periode)...
Für Teilaufgabe 2
Digitale Aufgabe
Tipp für Teilaufgabe 3
Um Teilaufgabe 3 zu lösen, kann dir diese gekürzte Version des Periodensystems helfen.
Schaue dir das Diagramm oder die Tabelle der Ionisierungsenergien an. Du kannst dir daraus, passend zu den Elementen, die Ionisierungsenergie für ein Elektron heraussuchen. Mit Hilfe der gekürzten Version des Periodensystem kannst du dann die Aufgabe leichter lösen.
Erinnerung: Die Ionisierungsenergie ist der Energiebetrag, der benötigt wird, um ein Elektron des entsprechenden Elements aus der Atomhülle zu entfernen.
Für Interessierte
Besondere Zustände
Sicher ist dir schon aufgefallen, dass die Ionisierungsenergie innerhalb einer Periode von links nach rechts nicht gleichmäßig ansteigt, sondern dass es Elemente gibt, bei denen die Ionisierungsenergie einen deutlichen "Knick" hat. Sie haben eine geringere Ionisierungsenergie als das Element davor. Sie passen nicht in den Trend.
In der 2. Periode sind das die Elemente Bor und Sauerstoff, in der 3. Periode Aluminium und Schwefel. Dieser Trend setzt sich in den folgenden Perioden fort: Die Elemente der 3. Hauptgruppe und die der 6. Hauptgruppe haben deutlich geringere Ioniserungsenergien als anzunehmen wäre. Das 1. Elektronen lässt sich bei diesen Elementen also leichter entfernen, es ist weniger stark an das Atom gebunden als bei den "Nachbarelementen".
Das Diagramm zeigt uns, dass die Elektronen, welche man zuerst aus dem Atom eines Elements entfernen kann, unterschiedlich stark an den Kern gebunden sein müssen. Um das erste Elektron aus einem Neonatom zu entfernen brauchen wir fast doppelt so viel Energie (21,6 eV) wie für das erste Elektron aus einem Kohlenstoffatom (11,3 eV). Die Atomhüllen der Elemente müssen sich also irgendwie voneinander unterscheiden.
Um den Aufbau der Atomhülle zu untersuchen schauen wir uns jetzt die Ionisierungsenergien eines Elements genauer an. Bisher haben wir nur die Energie betrachtet, die notwendig ist, um ein Elektron aus dem Atom zu entfernen. Wenn ein Elektron nach dem anderen aus dem Atom entfernt werden soll, kann die Energie für jedes Elektron bestimmt werden, bis alle Elektronen aus dem Atom entfernt worden sind.
Im folgenden Diagramm sind diese Ionisierungsenergien für Phosphor dargestellt. Ein Phosphoratom besitzt 15 Elektronen.
Aufgabe 7.2.3
- Formuliere schriftlich eine Beschreibung des Diagramms.
- Tipp: Das Arbeitsblatt "Strategie zur Beschreibung eines Diagramms" kann dir dabei helfen.
- Achte darauf, dass du nur beschreibst und nicht auswertest.
Die Balken im Diagramm entsprechen immer der Energiemenge, die für die Abspaltung des 1., 2., 3. usw. Elektrons nötigt ist.
Wir können erkennen, dass die Abspaltung jedes weiteren Elektrons immer schwieriger wird. Das lässt sich auch leicht begründen: Immer weniger Elektronen werden von der positiven Ladung des Kerns angezogen. Diese bleibt gleich. Auffällig ist, dass die Zunahme einen großen Sprung nach dem 5. und nach dem 13. Elektron macht.
Das zeigt uns, dass die Elektronen in einem Atom sich in ihrem Energiegehalt voneinander unterscheiden. Man sagt: Sie befinden sich auf unterschiedlichen Energiestufen. Anscheinend gibt es also Energiestufen, von denen die Elektronen leichter zu lösen sind als von anderen Energiestufen.
Um diese Energiestufen zu veranschaulichen, stelle dir vor, das ein Elektron ein Stein auf einer Leiter mit einer bestimmten Anzahl an Stufen wäre. Wenn ein Stein auf einer niedrigen Stufe ist (er ist also nah am Boden), ist noch viel Energie nötig, um den Stein über die ganzen Stufen der Leiter hinweg hochzuheben. Wenn du genug Energie aufwendest, ist der Stein irgendwann gar nicht mehr auf der Leiter, er ist ganz entfernt worden. Bezogen auf ein Atom bedeutet das: Wenn das Elektron auf einer niedrigen Energiestufe ist, also nah am Kern ist, ist viel Energie nötig, um es aus der Atomhülle zu entfernen. Wird genug Energie aufgebracht, kann wie der Stein auch, das Elektron ganz entfernt werden und ist dann nicht mehr Teil der Atomhülle.
Nun stellt sich aber die Frage: Wie können wir uns diese Energiestufen noch genauer vorstellen und wie verteilen sich die Elektronen eigentlich, wenn es mehr als ein Elektron in der Atomhülle gibt?
Die Antwort auf diese Frage findest du in Baustein 7.3.