Research
Research
Stochastic Thermodynamics
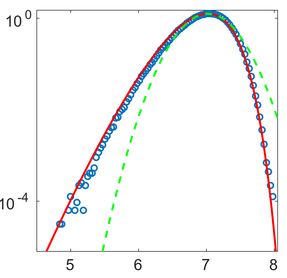Thermodynamic quantities of small systems fluctuate: an experiment performed repeatedly under identical conditions produces different values of work, heat, and entropy production each time. Accordingly, the thermodynamics of small systems rests on the analysis of probability distributions of thermodynamic quantities. Contrary to traditional statistical mechanics valuable physical information on the system under considerations is often contained in the large-deviation tails of these distributions. Using methods and techniques of stochastic thermodynamics we investigate the tails of work distributions in classical stochastic systems, the role of information as a thermodynamic resource, applications of large-deviation theory to hydrodynamic systems and the potential use of fluctuation theorems in Bayesian statistics.
Collective phases in models of biodiversity
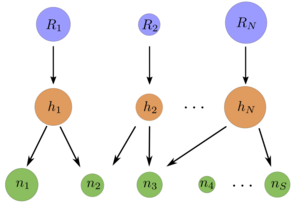Mathematical models of ecological systems have a long history dating back to the 19th century. Until recently, however, their explicit and detailed analysis was mostly confined to situations involving just a few species. On the other hand it is well known, that in real biological settings several hundred species compete and interact with each other. Rather few results are available at present concerning the properties of mathematical models with such a large number of species. Modeling the complex interactions between the various species by random matrices methods from the statistical mechanics of disordered systems may be used to characterize the typical properties of large ecosystems. Along these lines we investigate the emergence of cooperative phases in systems of purely competing species above a certain threshold of biodiversity.
The emergence of thermodynamics in isolated quantum systems
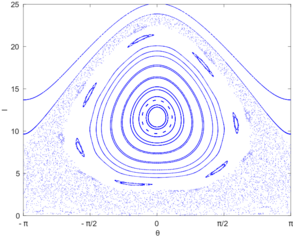The approach of quantum systems to a steady long-time limit is a classical problem and key issue in different areas of modern many-body physics. In particular, the process of equilibration, although prerequisite for the tremendous success of equilibrium statistical mechanics, is in many aspects poorly understood at present. There is a recent upsurge of interest in these questions related to the concepts of eigenstate thermalization and typicality of pure quantum states. Within the Research Unit 2692 of the German Science Foundation we investigate the relationship between definitions of work in small driven classical and quantum systems by using semi-classical techniques with special emphasis on classically chaotic systems.