Variational EM for Big Fast Clustering
Contact
Head of lab
Lab Administration
Postal Address
Office Address
Variational EM for Big Fast Clustering
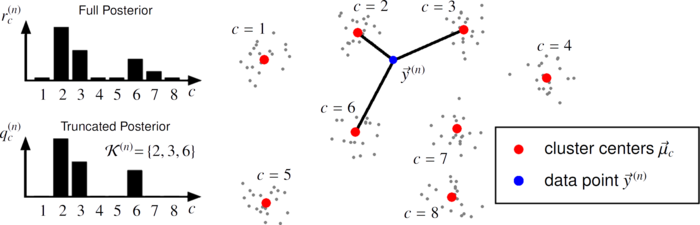
Illustration of truncated distributions for a GMM in D = 2 dimensions. The figure considers a data point \(\vec{y}^{(n)}\) which lies (for illustrative purposes) to some extend in between some clusters. For C = 8 cluster, the full posterior (aka. the responsibilities) \(r_c^{(n)} = p(c | \vec{y}^{(n)},Θ)\) are shown in the top-left. Below, a truncated approximation \(q_c^{(n)}\) with |K| = C' = 3 is shown for the same data point. The truncated approximation maintains the C' highest posterior values, sets all others to zero, and renormalizes the distribution to sum to one. The three closest clusters, which correspond to the three highest posterior values, are connected with black lines in the main figure.
Announcement of Future Updates
We are currently undertaking both technical and scientific improvements for the optimization of mixture models at very large scales. On the software side, the updates in development include the following:
- Performance: Overall improvements, including enhanced shared memory parallelization.
- Simplified Installation Process: To get up and running quickly with an easier installation procedure.
- User-Friendly Interface: An intuitive and streamlined Python interface for easier applicability.
- Enhanced Documentation: A more comprehensive documentation to further support the use of our algorithms.
Future results will be communicated through scientific papers, and the associated algorithms will be released upon publication.
If you are interested in large-scale mixture models and clustering and wish to try out our algorithms prior to their release, please contact us via E-Mail: till.kahlke@uol.de
Description
In this line of research, we investigate novel variational approaches to decisively improve learning algorithms for clustering. We are interested in the theoretical as well as practical aspects of such approaches.
In practice, variational approaches allow for the derivation of very efficient clustering algorithms for large-scale problems, i.e., when the number of clusters and the number of data points is large, and when the dimensionality of data points is high. Variational approaches can, in this respect, provide a very favorable scaling behavior with the number of clusters. Such a scaling can then be combined with approaches developed by other groups that allow for favorable scaling with the number of data points (e.g. coreset approaches) or the data dimensionality (e.g., by exploiting triangle inequalities).
On the theoretical side, the variational approaches we investigate allow the definition of learning algorithms that interpolate between hard EM clustering approaches (such as k-means) and soft-EM clustering as, e.g., provided by EM for Gaussian mixture models (GMMs). The illustration above shows, for instance, a k-means-like algorithm based on three instead of one 'winning' cluster (this is an instance of the k-means-C' algorithm [Lücke & Forster, 2019] with C' = 3). In the framework of variational EM, k-means is itself obtained as a limit case of the k-means-C' algorithm (namely when C' = 1). As a consequence, k-means (Lloyd's algorithm) can be obtained as an approximation of EM for GMMs without the requirement to take a limit to small or zero cluster variances (which is the usual textbook approach). This implies further, that k-means optimizes a variational lower bound (i.e. a free energy a.k.a. ELBO) of a GMM loglikelihood. The paper [Lücke & Forster, 2019] provides a number of quantitative results on the relation of k-means algorithms to GMM data models including a formula to directly translate the quantization error to a variational lower bound. [Lücke & Forster, 2019] is itself based on more general theoretical results about the family of truncated posteriors as variational distributions [Lücke, 2019].
Based on variational EM interpretations of k-means-like algorithms, accelerations of clustering algorithms can be obtained by defining partial instead of full variational E-steps. Variational lower bounds can then be increased without having to compute the distances of a given data point to all cluster centers. In the paper [Forster & Lücke, 2018] it was shown that such partial E-steps can be defined independently of the number of clusters. As a consequence, the number of required distance evaluations could (for clustering problems with many clusters) be drastically reduced. That the number of strongly reduced distance evaluations translates into algorithms that are in practice also strongly improving the state-of-the-art efficiency was then shown by the paper [Hirschberger et al., 2022]. The paper showed for large-scale problems that (A) the reduction of distance evaluations clearly outweighs to memory overhead and auxiliary computations required to implement the variational EM procedure, and (B) that the variational complexity reduction can be combined with complexity reduction approaches for large data sets (we used coresets) and complexity reduction for large data dimensionality (we used the triangle inequality).
A list of our so-far published clustering algorithms together with their implementations is provided below. Implementations based on python are primarily of interest for the theoretical studies [Lücke & Forster, 2019; Forster & Lücke, 2018] . The python implementations can readily be used in relation to theoretical studies, e.g., on convergence properties or for comparisons with k-means-like algorithms. They are, however, not optimized for execution times or large data sets. The implementations based on C++ were optimized both in terms of memory I/O efficiency and run-time efficiency. Furthermore, their more hardware-near C++ code is supporting fast computation time. The algorithm vc-GMM is only available as C++ implementation and, most importantly, contain combinations with fast-seeding, fast coreset construction, and efficient computations for high data dimensionalities. This algorithm stand to compete as the fastest clustering algorithms for very large-scale clustering problems.
Algorithms
| Algorithm | Implementation | Reference |
| k-means-C' | Python Code Repository (not optimized*) | Lücke & Forster, 2019 |
| var-k-means-X | Python Code Repository (not optimized*) | Forster & Lücke, 2018 |
| var-k-means-S | Python Code Repository (not optimized*) | Forster & Lücke, 2018 |
| var-GMM-X | Python Code Repository (not optimized*) | Forster & Lücke, 2018 |
| var-GMM-S | Python Code Repository (not optimized*) C++ Code Repository (optimized) | Forster & Lücke, 2018 Hirschberger et al., 2022 |
| vc-GMM | C++ Code Repository (optimized) | Hirschberger et al., 2022 |
*the Python code is not optimized for real-time execution speed, but for analysis and research only.
References (own publications)
[Hirschberger et al., 2022]
A Variational EM Acceleration for Efficient Clustering at Very Large Scales
Florian Hirschberger*, Dennis Forster*, Jörg Lücke.
IEEE Transactions on Pattern Analysis and Machine Intelligence 44(12):9787-9801, 2022.
*joint first authors.
[Lücke & Forster, 2019]
k-means as a variational EM approximation of Gaussian mixture models
Jörg Lücke and Dennis Forster, Pattern Recognition Letters, 2019.
[Lücke, 2019]
Truncated Variational Expectation Maximization
Jörg Lücke, arXiv:1610.03113, 2019.
[Forster & Lücke, 2018]
Can clustering scale sublinearly with its clusters? A variational EM acceleration of GMMs and k-means
Dennis Forster and Jörg Lücke, AISTATS, 2018.