Recent Announcements
Contact
Universität Oldenburg
Institute of Physics & ForWind
Küpkersweg 70,
26129 Oldenburg
Prof. Dr. Joachim Peinke
Room, W33 3-302
Fax. +49-(0)441-798-5099
Tel. +49-(0)441-798-5050
Sektr. +49-(0)441-798-5090
peinke@uol.de
Recent Announcements
On the contributions to statistical physics of Giorgio Parisi, Nobel Prize winner 2021
The importance of analyzing multifractal models in turbulence and financial data is also reflected in the recent publication on the 2021 Nobel Prize winner in physics.
Bremer Industry Talk with Prof. Joachim Peinke
In the video contribution of the Deutsche Physikalische Gesellschaft e.V., Joachim Peinke gives insights into the importance of turbulence research for the current energy transition in Germany.
The lecture covers both general and current research topics in the field of turbulence research.
Following the lecture, Prof. Peinke responds to previously submitted questions in a Q&A session.
Recent Announcements
Extracting dynamical cluster features of complex systems
In a recently published article Philip Rinn, Yuriy Stepanov, Joachim Peinke, Thomas Guhr and Rudi Schäfer propose to combine cluster analysis and stochastic process analysis to characterize high-dimensional complex dynamical systems by few dominating variables. They analyze stock market data for which the dynamical stability as well as transitions between different stable states are found. The method allows to set up new criteria for identifying spurious clusters and to uncover dynamically distinct states.
Dynamics of quasi-stationary systems: Finance as an example
P. Rinn, Y. Stepanov, J. Peinke, T. Guhr, und R. Schäfer
EPL (Europhysics Letters), vol. 110, iss. 6, p. 68003, 2015.
Detect mechanical damage at an early stage
Philip Rinn, Hendrik Heißelmann, Matthias Wächer and Joachim Peinke present in an article (description in pro-Physik and highlights in Europhysics News) a new method for diagnosing even the smallest changes in mechanical properties. Especially for reliable continuous operation of wind turbines, timely detection of mechanical damage is crucial. Here, the new method should enable better damage diagnosis of wind turbines.
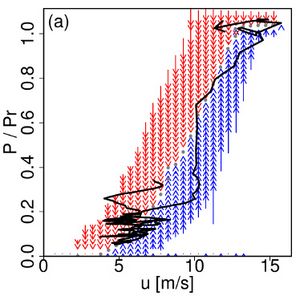
The turbulent character of wind energy
Patrick Milan, Matthias Wächer and Joachim Peinke describe in an article in the journal Physical Review Letters (description in Phys-org) that the energy conversion process on small time scales in the range of seconds follows complex patterns with multi-fractal scale laws, which correspond to the theory on turbulence of A. N. Kolmogorov from 1962.
Illustration of the second dynamics of the power output of a modern wind turbine. In the background the deterministic drift field of a reconstructed Langevin equation for the dynamics of the power conversion.