Bayesian Gaussian One- and Two-Parameter Models
Bayesian Gaussian One- and Two-Parameter Models
Bayesian Gaussian Models
One- and two-parameter Bayesian Gaussian models are models with a Gaussian likelihood (= Gaussian observation model). They are as stand-alone models of limited scientific value. Instead, their importance lies in being simple statistical building bricks in embracing bigger models to allow some 'finger exercises' or cognitive 'etudes' in model conception, data analysis, formula-based inference with conjugate priors, and simulation-based inference with a probabilistic programming language (PPL; e.g. TURING.jl). Because of their ubiquitousness the probability is high that these models can be found in libraries of other PPLs so that comparisons with respect to utility, comprehensability, and effectiveness are possible.
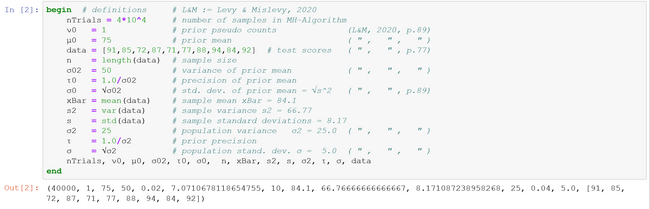
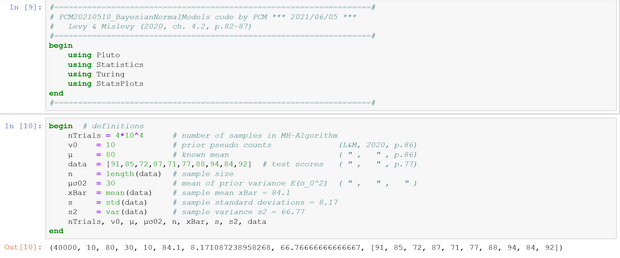
For the three model variants presented here, we use data examples from Levy & Mislevy (L&M, 2020, ch.4) to make comparisons between our TURING.jl and their WINBUGS-models possible. As a kind of \(\textit{specification}\) we use several parameter values either directly obtained from Levy & Mislevy or derived from their published Inverse-Gamma-(IG)-hyperparameters \(\alpha\) and \(\beta\) (see the table below).
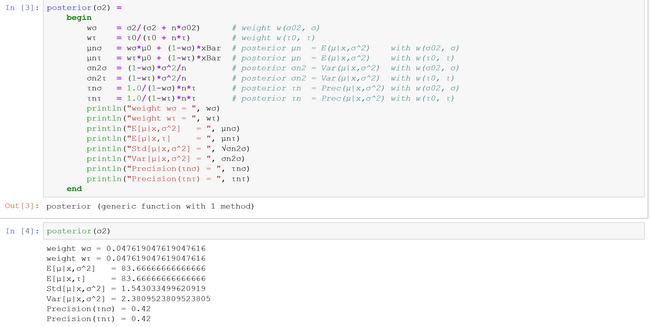
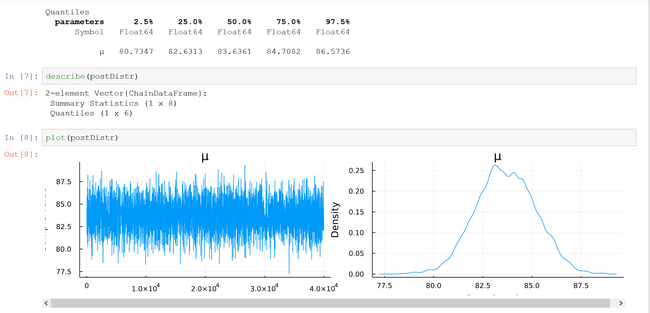
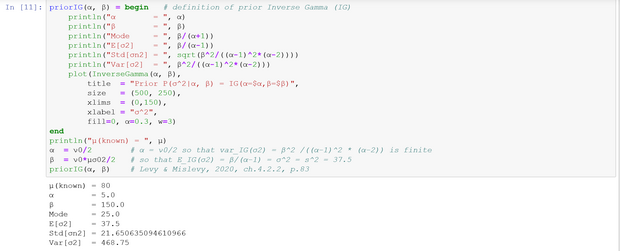
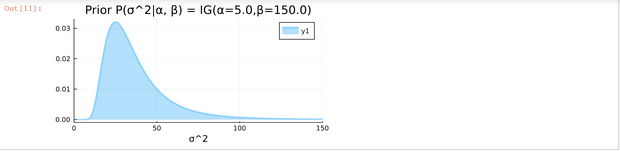
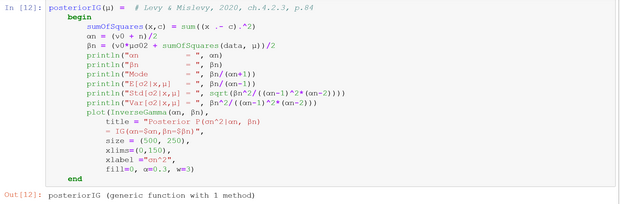
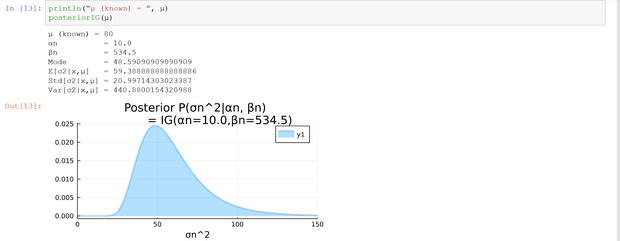
$$ \begin{array}{c|c|c|c} \text{model} & \text{known} & \text{unknown} & \text{L&M} \\ \hline 1. & \text{conjugate prior} & & \\ \hline prior & E(\sigma^2)=25.00 & E(\mu |\sigma^2 = 75.00 & (4.15), p.81 \\ & & Var(\mu|\sigma^2 = 50.00 & \\ & & Std(\mu|\sigma^2= 7.07 & \\ \hline posterior & E(\sigma^2)=25.00 & E(\mu| \mathbf{x}, \sigma^2)=83.67 & (4.16), p.81 \\ & & Var(\mu|\mathbf{x},\sigma^2)=2.37 & \\ & \mathbf{x} = (91,85,72,87,71,77,88,94,84,92) & Std(\mu|\mathbf{x},\sigma^2)=1.54 & \\ \hline 2. & \text{conjugate prior} & & \\ \hline prior & E(\mu)=80.00 & E(\sigma^2|\mu)=37.50 & (4.30), p.86 \\ & \alpha=5,\beta=150 & Var(\sigma^2|\mu)=468.75 & \\ & & Std(\sigma^2|\mu)=21.65 & \\ \hline posterior & E(\mu)=80.00 & E(\sigma^2|\mathbf{x},\mu)=59.39 & (4.31), p.87 \\ & \alpha=10, \beta=534.5 & Var(\sigma^2|\mathbf{x},\mu)=441.00 & \\ & \mathbf{x} = (91,85,72,87,71,77,88,94,84,92) & Std(\sigma^2|\mathbf{x},\mu)=21.00 & \\ \hline \end{array} $$
All specifications could be regenerated by our Turing.jl/IJulia scripts (see below).
References
LEVY, R. & MISLEVY, R.J., Bayesian Psychometric Modeling, Boca Raton, Fl.: CRC Press 2020
------------------------------------------------------------------------------------------
This is a draft. Comments or hints for bug fixes are welcome:
Prof. Dr. Claus Möbus: claus.moebus@uol.de
-------------------------------------------------------------------------------------------
1. One-Parameter Model: Unknown Mean and Known Variance
-------------------------------------------------------------------------------------------
This is a draft. Comments or hints for bug fixes are welcome:
Prof. Dr. Claus Möbus: claus.moebus@uol.de
-------------------------------------------------------------------------------------------
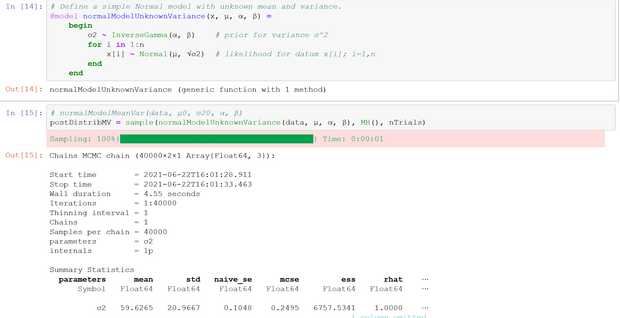
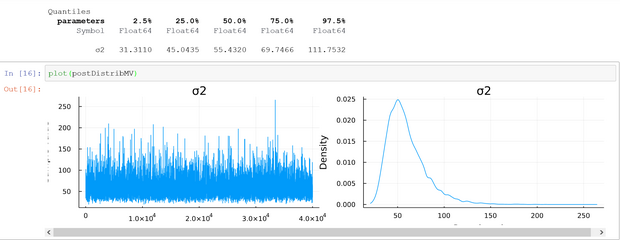
2. One-Parameter Model: Known Mean and Unknown Variance
-------------------------------------------------------------------------------------------
This is a draft. Comments or hints for bug fixes are welcome:
Prof. Dr. Claus Möbus: claus.moebus@uol.de
-------------------------------------------------------------------------------------------
3. Two-parameter Model: Unknown Mean and Variance
-------------------------------------------------------------------------------------------
This is a draft. Comments or hints for bug fixes are welcome:
Prof. Dr. Claus Möbus: claus.moebus@uol.de
-------------------------------------------------------------------------------------------