Lesson3: Particle Filter - Resampling -
Lesson3: Particle Filter - Resampling -
Resampling with Normalized Alpha-Weights (WebChurch)
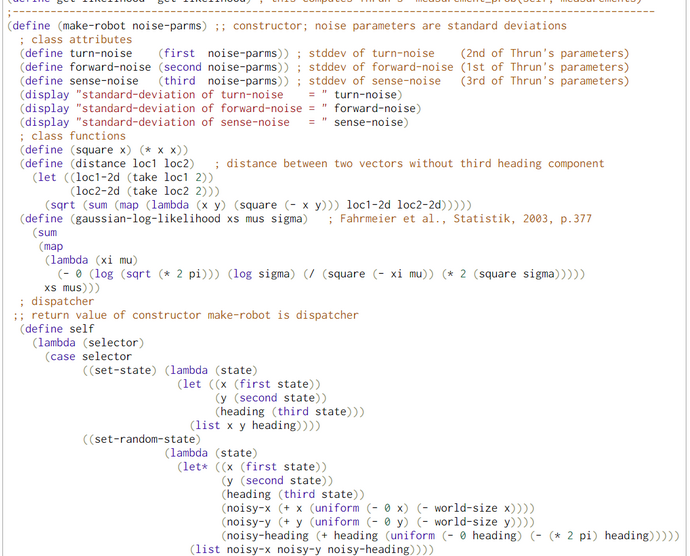
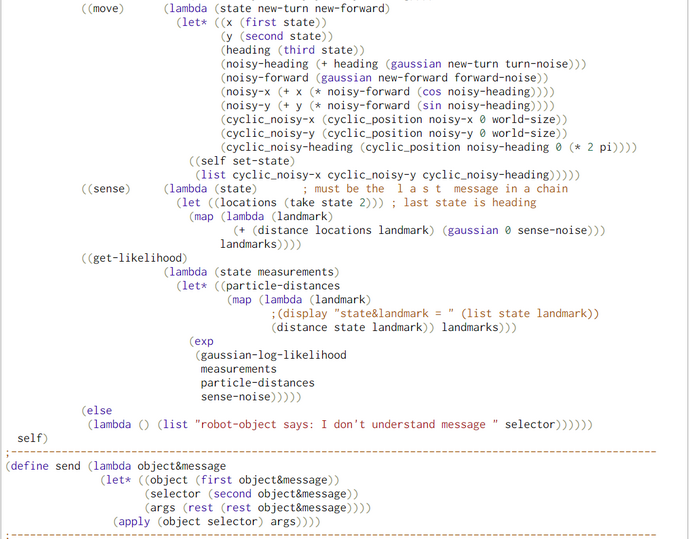
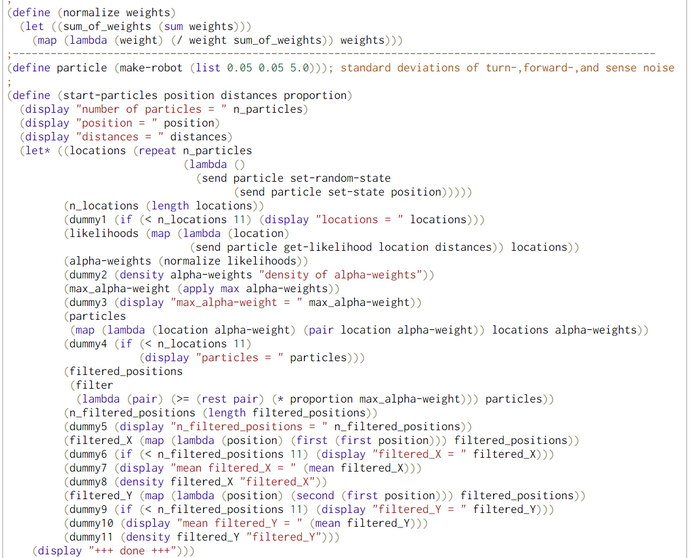

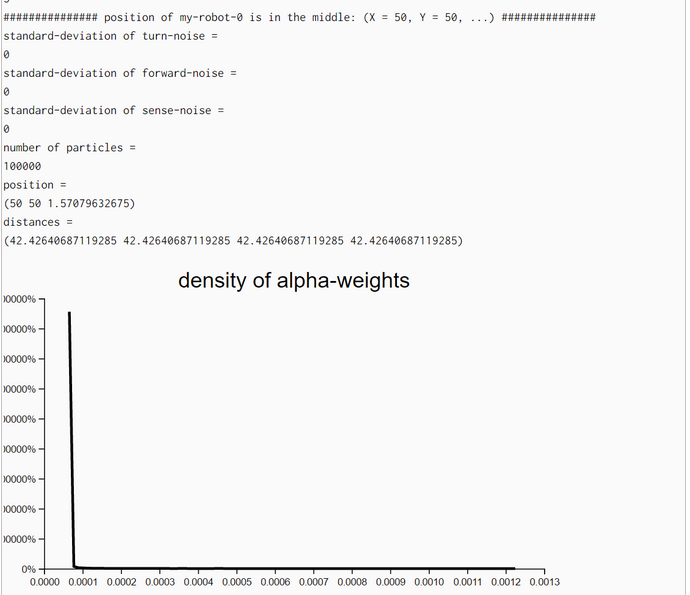
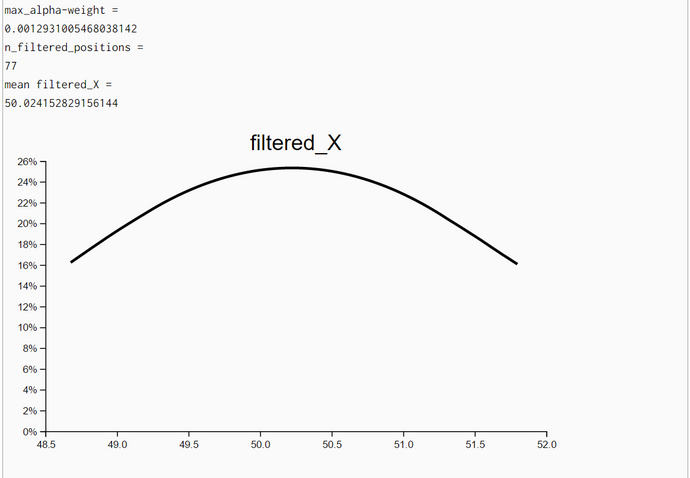
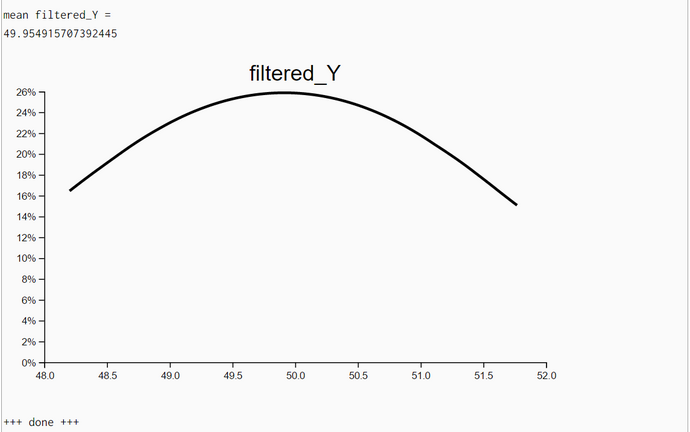
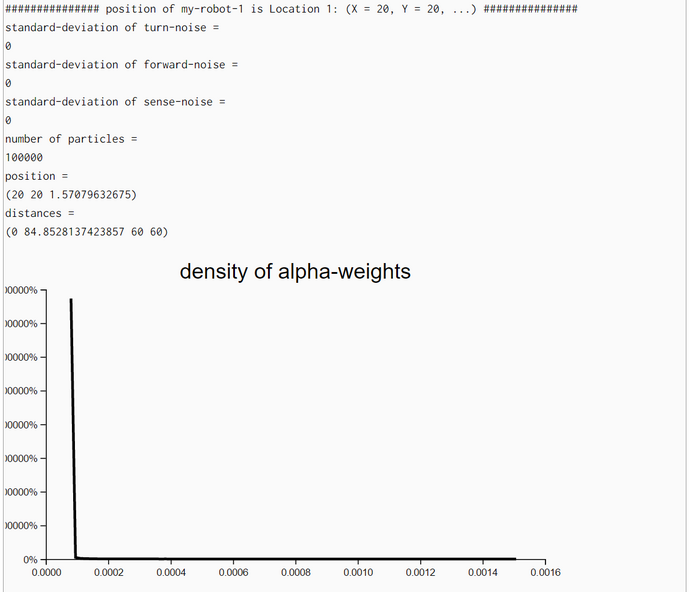
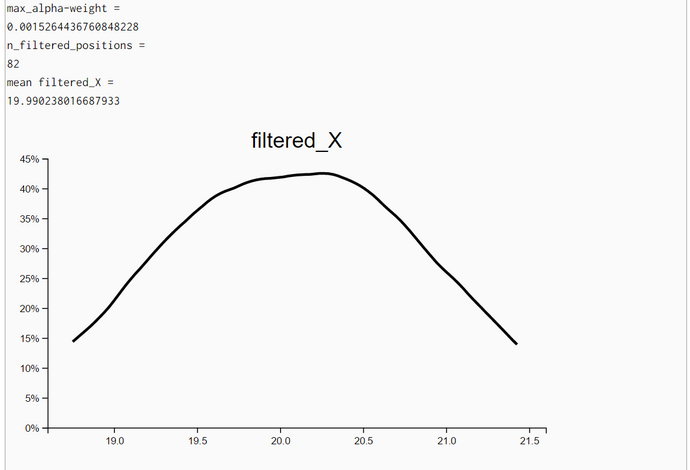
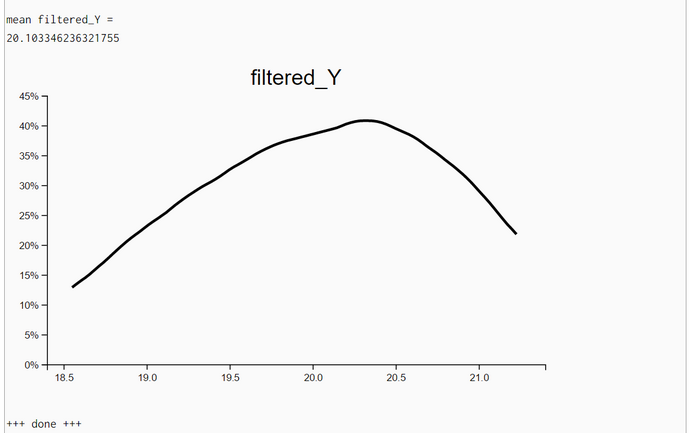
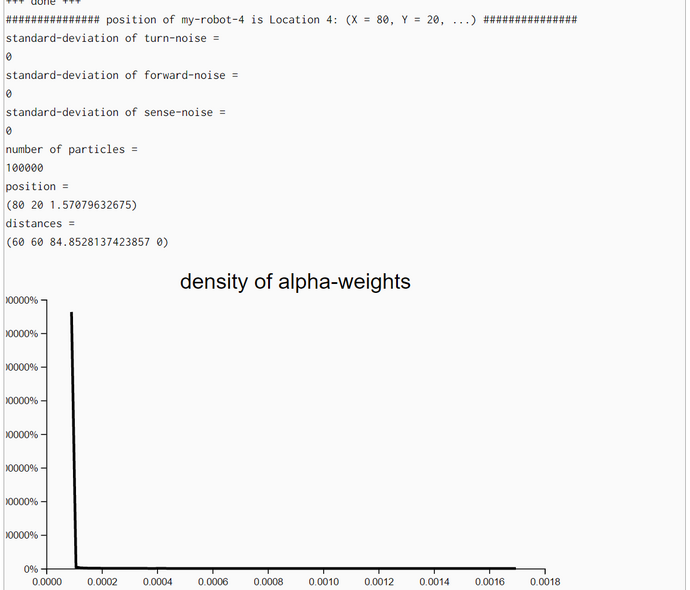
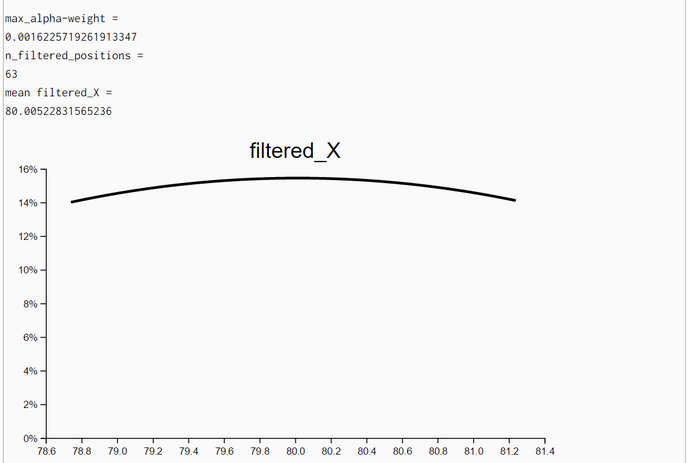
Particle Filter Algorithm without Movement but with Iteration (WebChurch)
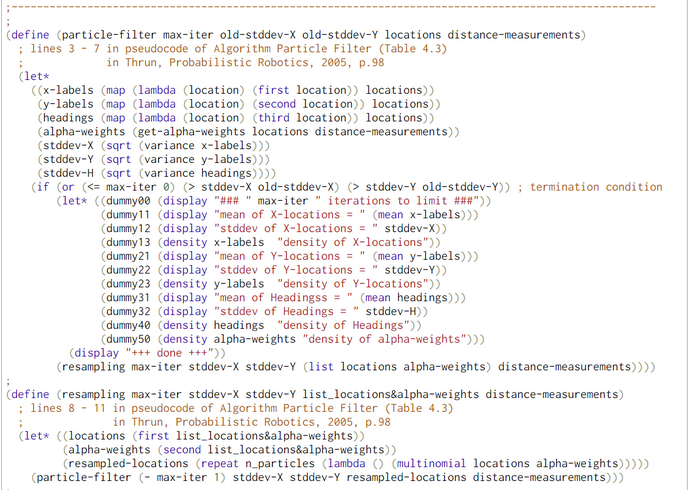
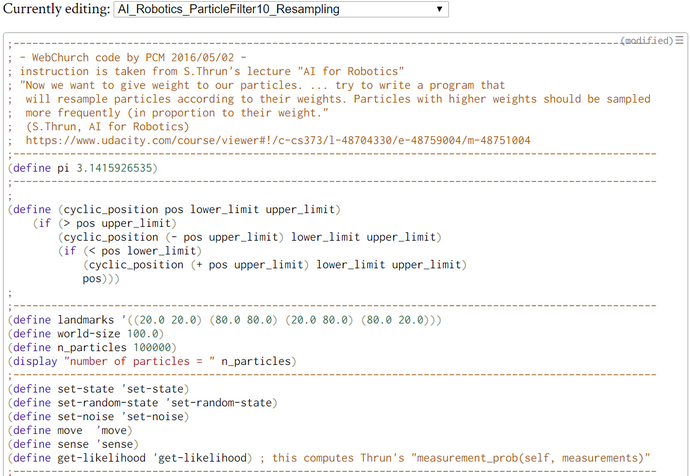
Our WebChurch code implements the algorithm Particle-filter (Table 4.3 in Thrun et al., Probabilistic Robotics, 2005, p.98) but without movement u(t) and only one measurement z(t). In contrast to that latter pseudocode we implemented an iteration scheme to explore the possibility of iterative improvement.
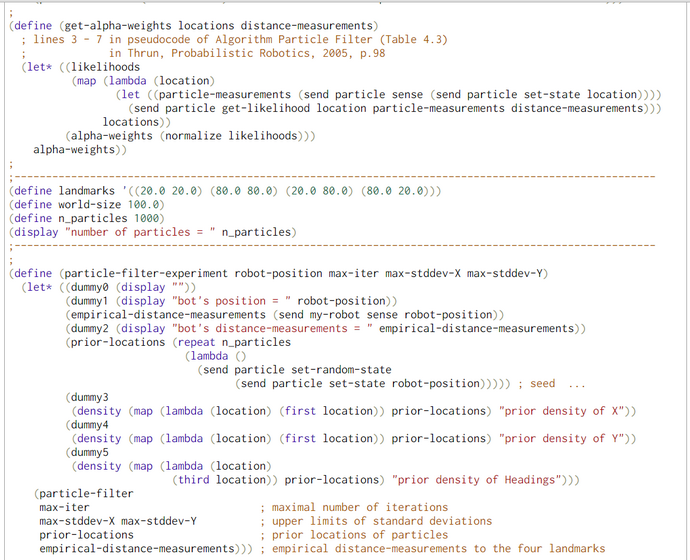
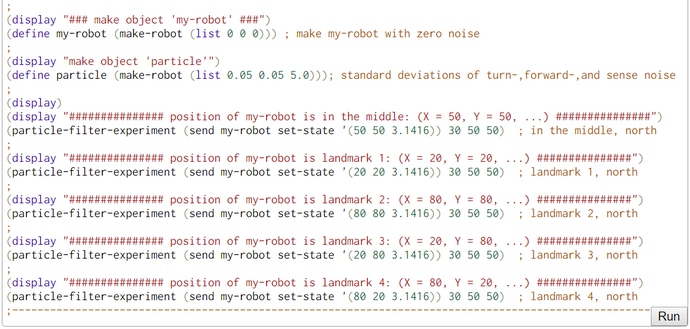
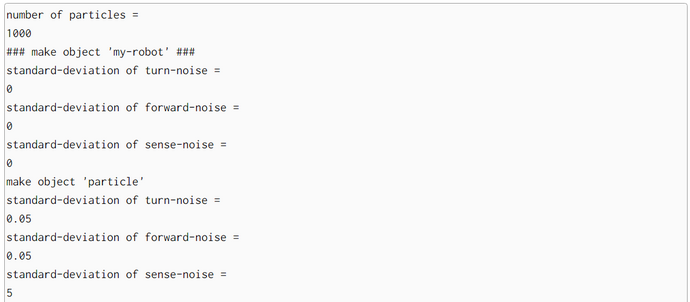
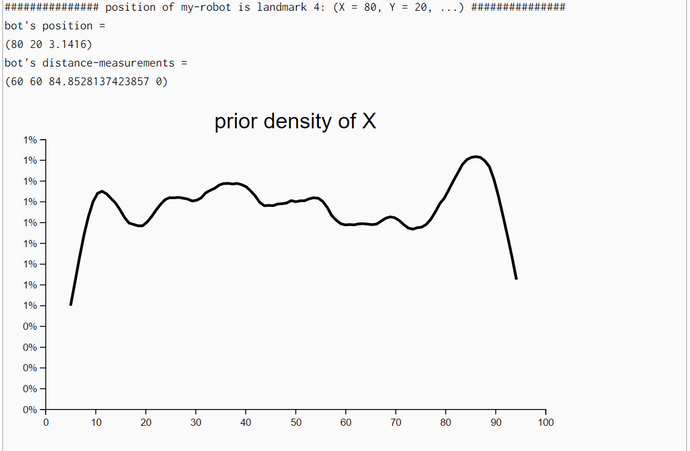
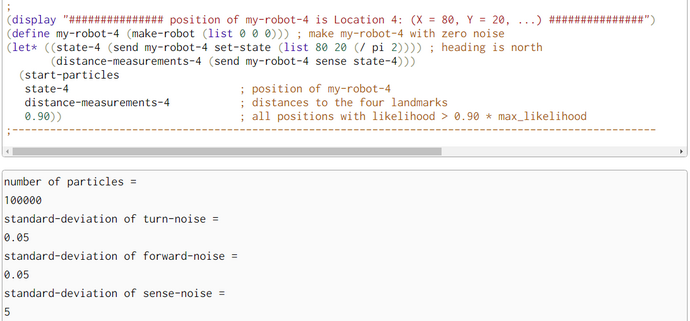
We conducted with the help of function particle-filter-experiment (pfe) five simulation experiments. The first argument of pfe is the position of the bot. The other three are technical arguments which are explained in the comments. In the first part of pfe the prior locations of the particles and the empirical distance measurements of the bot are generated.
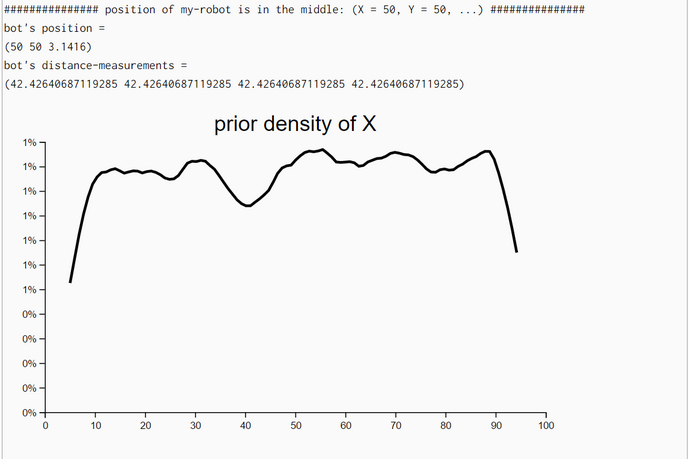
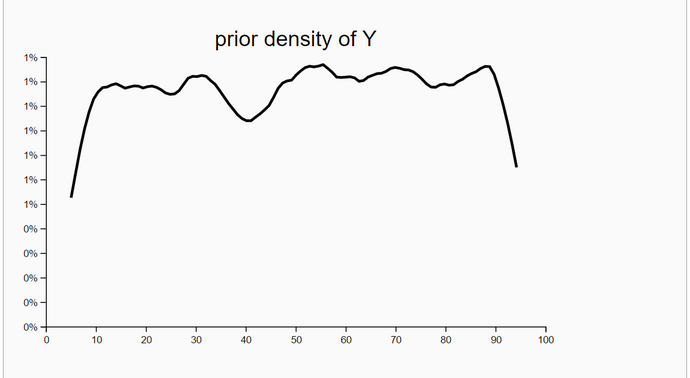
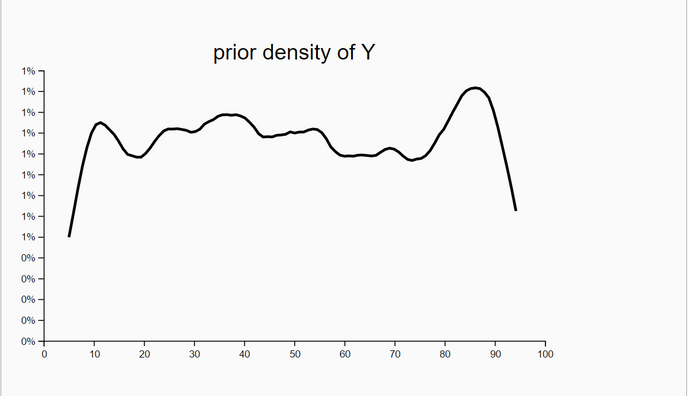
For the locations of the particles we chose a 2D-uniform distribution so that the seed points for the particles are rather uniform distributed accross the bot's world. Only for the generation of the empirical distance measurements we need the position of the bot. His position consists of his location (X- and Y-coordinate) and his heading.
The second part of pfe consists of a call to the function particle-filter (pf). Besides some technical arguments pfe only takes the locations (X in Thrun's pseudocode) of the particles and the empirical distance measurements (Z in Thrun's pseudocode) as arguments. Because we study the behavior of the pf without bot-movement we have no argument and no parameter for the bot's movement (u in Thrun's pseudocode)
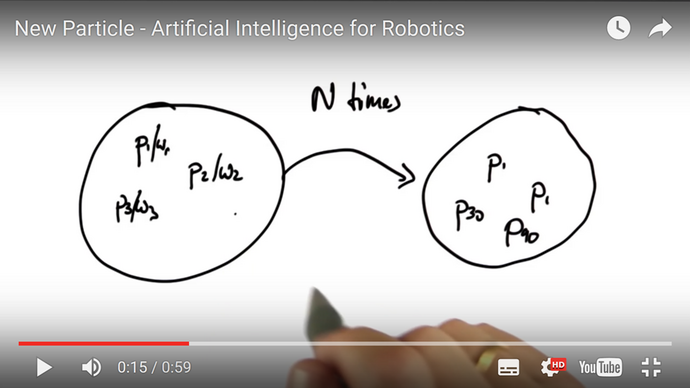
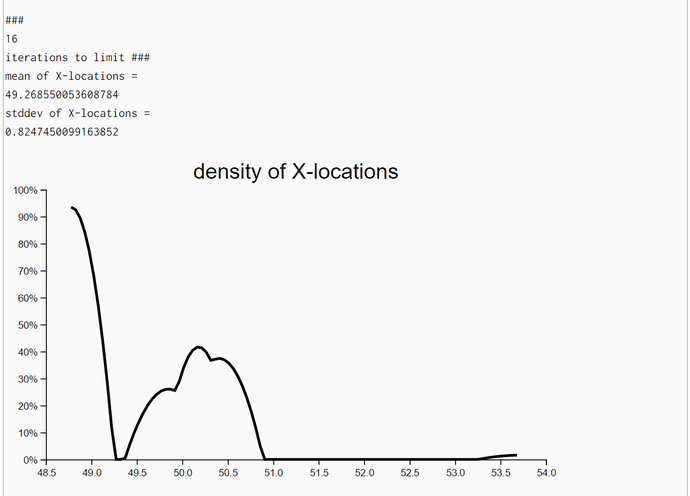
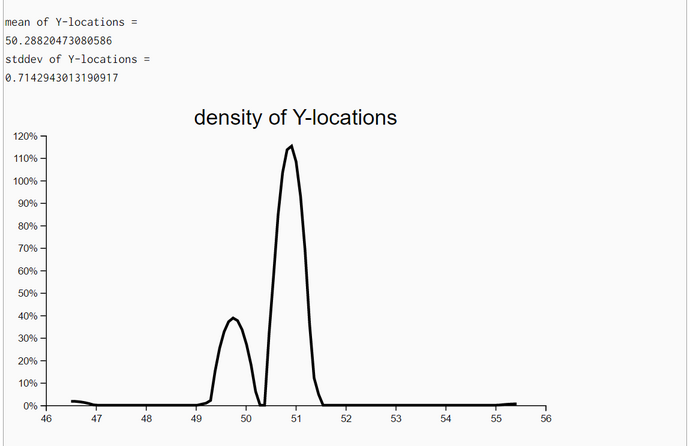
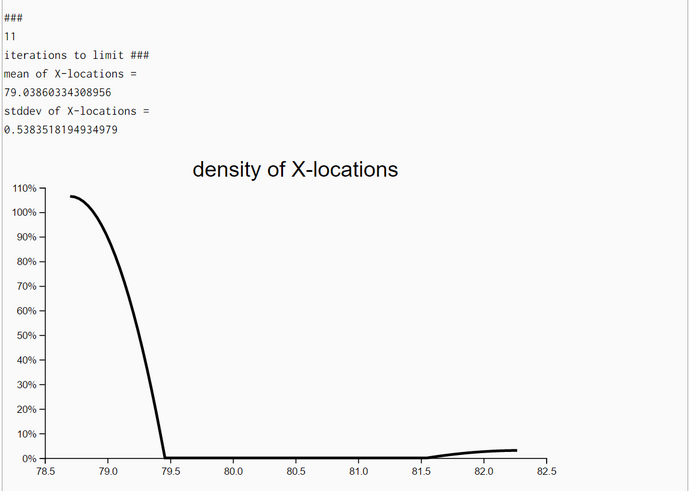
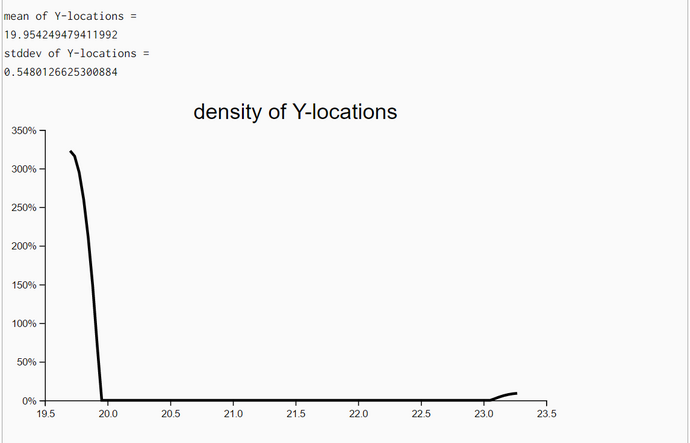
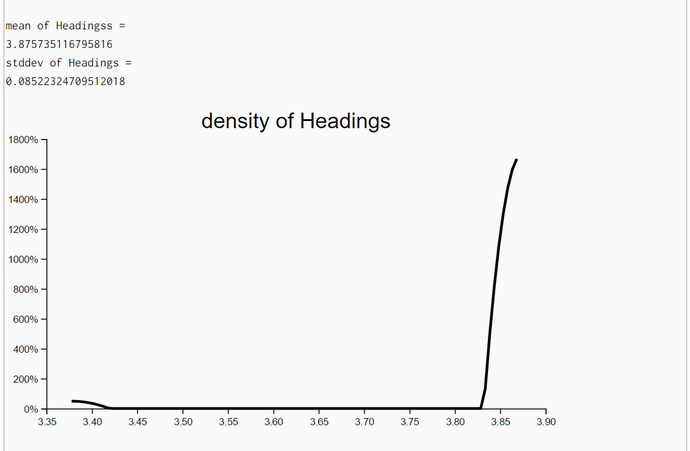
The density plots of unweighted resampled X- and Y-locations demonstrate that the posterior locations X and Y do improve substantially when we iterate the particle-filter algorithm with the same set of measurements. A new iteration with the same set of measurements started when both standard deviations (of X and Y coordinates) improved between the last and current step and the upper limit of iterations (her: 20) has not been reached.
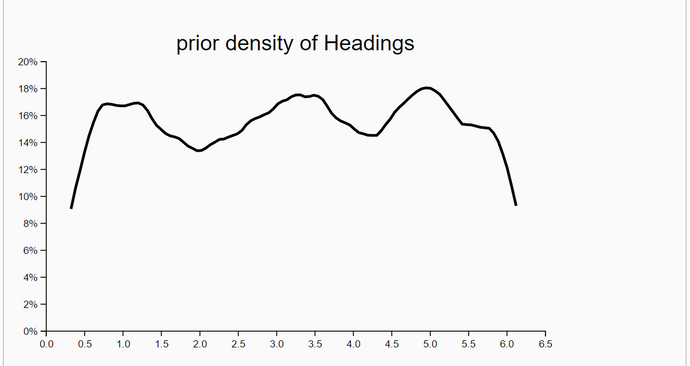
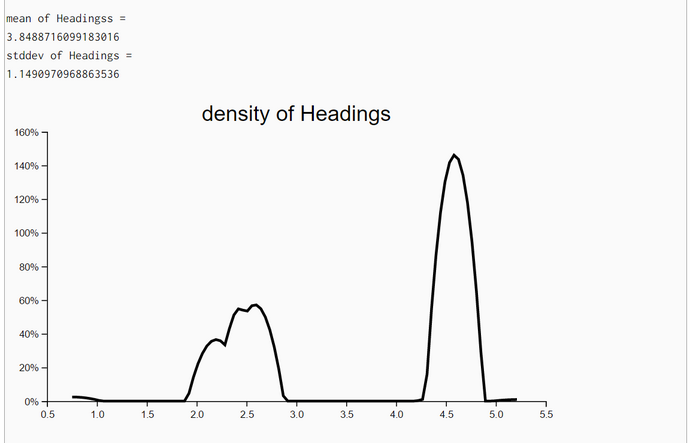
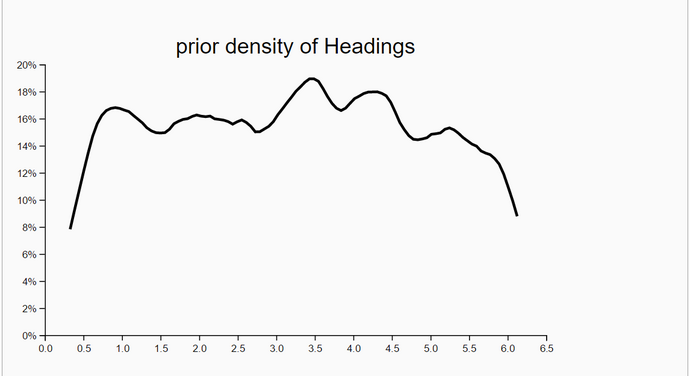
In the first experiment 13 iterations showed improvement and in the second experiment we used the full set of 20 iterations. We even plotted the densities of headings though the likelihood of locations is independent of headings. We have no explanation why the posterior densities have a smaller standard deviation than the corresponding prior density of Heading.
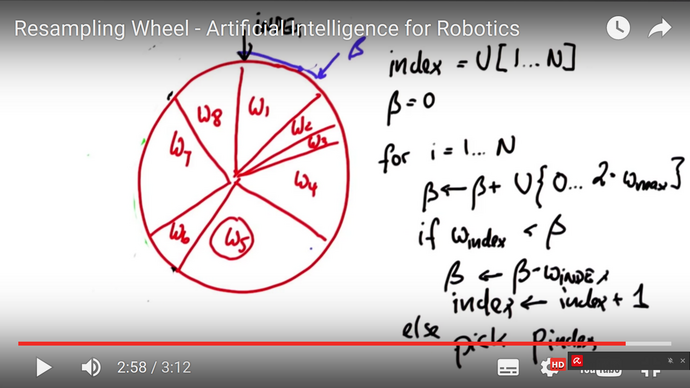
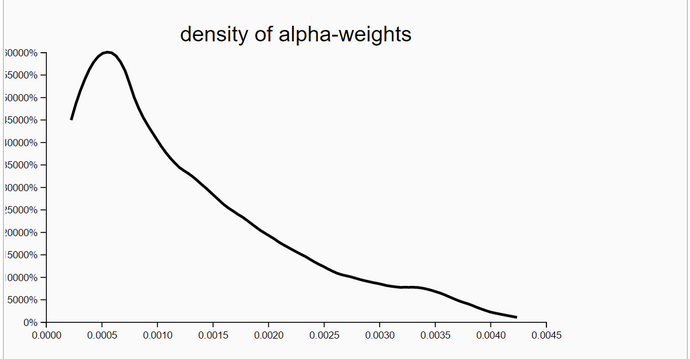
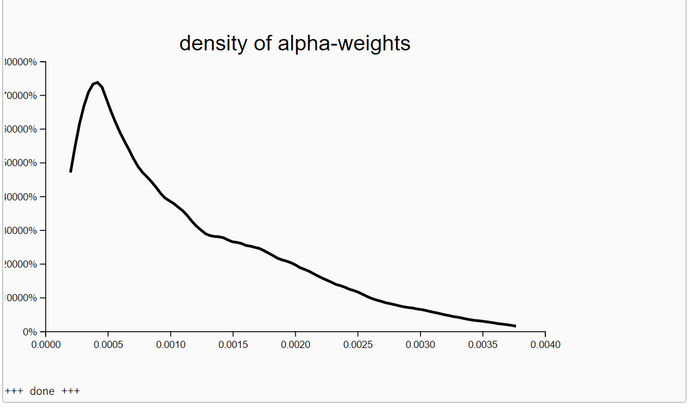
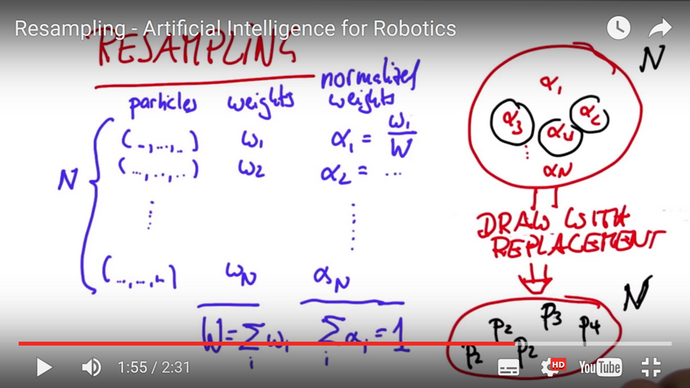
In his lecture Thrun recommends a so called resampling wheel (www.udacity.com/course/viewer#!/c-cs373/l-48704330/e-48748082/m-48740082). We replaced his resampling wheel by sampling locations using a multinomial random number generator (multinomial <list_of_locations> <list_of_alpha_weights>).