01_Measurement Update
01_Measurement Update
Lesson1: Localization - Uniform Distribution - (WebChurch)
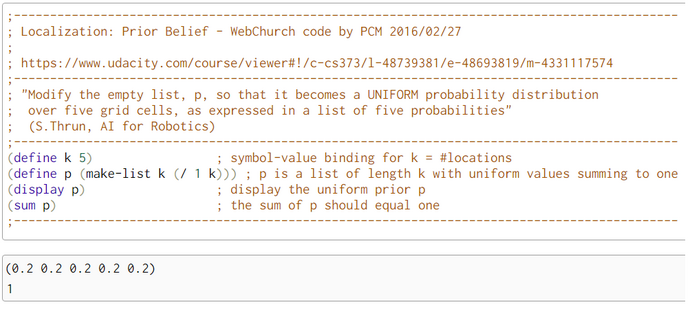
;-----------------------------------------------------------------------------------
; Localization: Prior Belief - WebChurch code by PCM 2016/02/24
; - instruction by S.Thrun, AI for Robotics -
; www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48693819/m-4331117574
;-----------------------------------------------------------------------------------
Lesson1: Localization - Generalized Uniform Distribution - (WebChurch)
;-----------------------------------------------------------------------------------
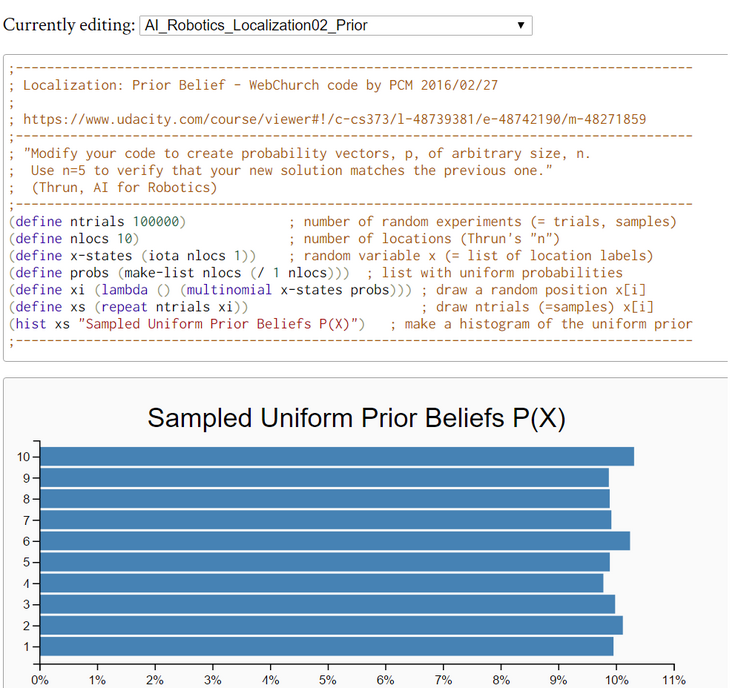
; Localization: Prior Belief - WebChurch code by PCM 2016/02/24
; - instruction by S.Thrun, AI for Robotics -
; www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48742190/m-48271859
;-----------------------------------------------------------------------------------
Lesson1: Localization - Normalized Posterior Distribution - (WebChurch: rejection-query)
;-------------------------------------------------------------------------------------------------------
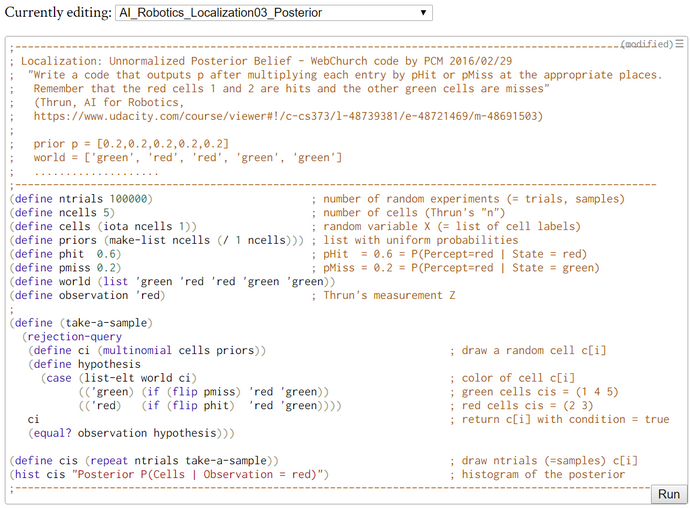
; Localization: Normalized Posterior Belief - WebChurch code by PCM 2016/02/28
; instruction by Thrun, AI for Robotics,
; www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48721469/m-48691503
;-------------------------------------------------------------------------------------------------------
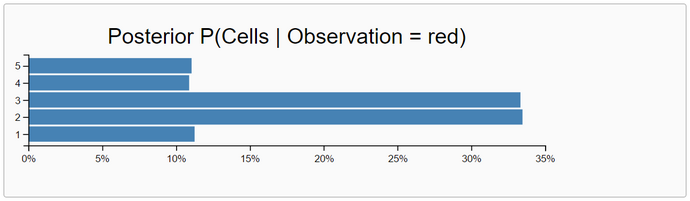
Here, we use the approximative rejection-query algorithm.
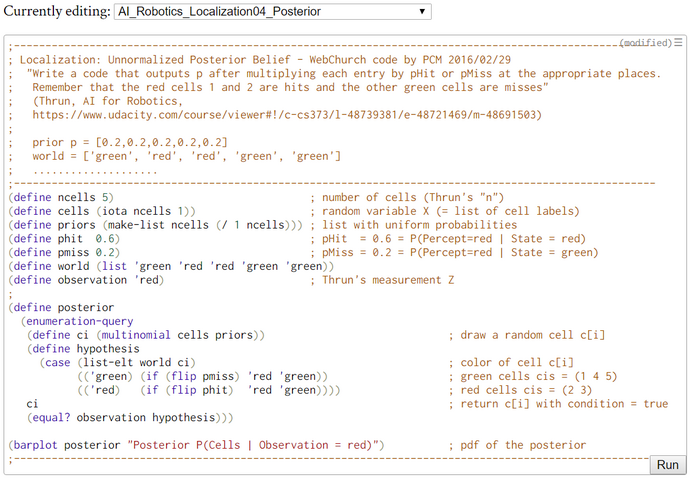
Lesson1: Localization - Normalized Posterior Distribution - (WebChurch: enumeration-query)
<link typo3/sysext/cms/layout/db_layout.php?id=45718# - - Bearbeiten>;-------------------------------------------------------------------------------------------------------
; Localization: Normalized Posterior Belief - WebChurch code by PCM 2016/02/28
; instruction by Thrun, AI for Robotics,
; </link>www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48721469/m-48691503
;-------------------------------------------------------------------------------------------------------
Here, we use the exact enumeration-query algorithm.
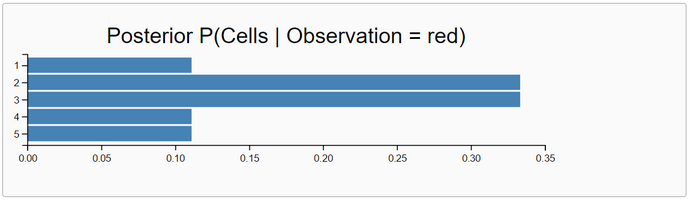
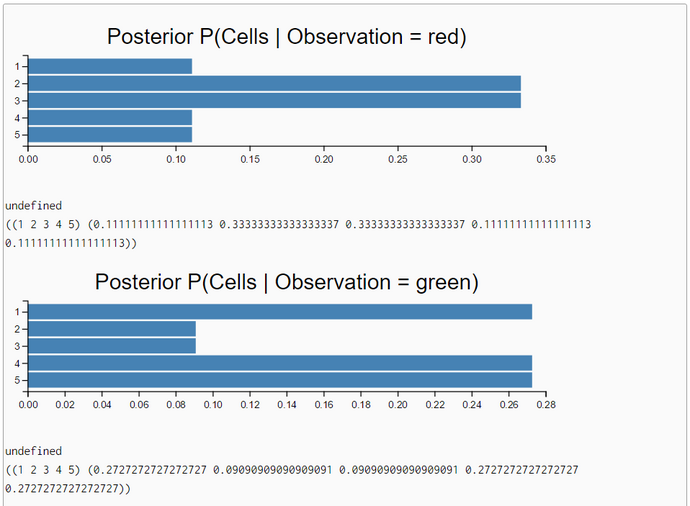
Lesson1: Localization - Measurement Update with Sense - (WebChurch: enumeration-query, function combination)
;------------------------------------------------------------------------------------------------------
; Localization: Measurement Update with Sense Function - WebChurch code by PCM 2016/03/02 -
; instruction by Sebastian Thrun, AI for Robotics,
; www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48692806/m-48641537)
;------------------------------------------------------------------------------------------------------
In this section we deal with the measurement update of a prior belief distribution. This is an important step in the Bayes filter algorithm (Thrun, Burgard & Fox, 2005, p.27). In his Python code Thrun uses a classical nonsampling approach. To get the posterior probabilities of state localization he multiplies in his Udacity lecture the prior probabilities with weights pHit = 0.6 and pMiss = 0.2. These numbers cannot
| weight | world[i]=red | world[i]=green | sum |
| Z = red | pHit = 0.6 | pMiss = 0.2 | 0.8 |
| Z = green | pMiss = 0.2 | pHit = 0.6 | 0.8 |
| sum | 0.8 | 0.8 | 1.6 |
be interpreted as probabilities because they don't add up to one.
In the sampling programs of our generic Bayesian models we need normalized conditional probabilities. There are two alternatives. First, we can normalize pHit and pMiss before using them in the sampling process:
| P(Z | world[i]) | world[i]=red | world[i]=green |
| Z = red | pHit = 0.6/0.8 = 0.75 | pMiss = 0.25 |
| Z = green | pMiss = 0.2/0.8 = 0.25 | pHit = 0.75 |
| column sum | 0.75 + 0.25 = 1.00 | 1.00 |
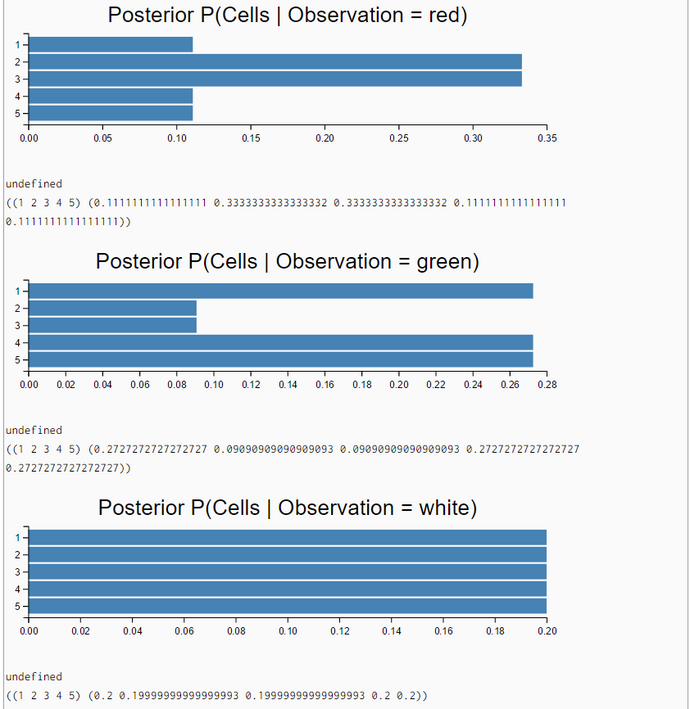
or second, we leave Thrun's weights unchanged and introduce a third measurement category Z = white. This third category receives conditional probabilities P(Z = white | world[i]) = (1 - pHit - pMiss) = 0.2. The second alternative is shown in the next display. Both methods generate posterior distributions which are identical with Thrun's.
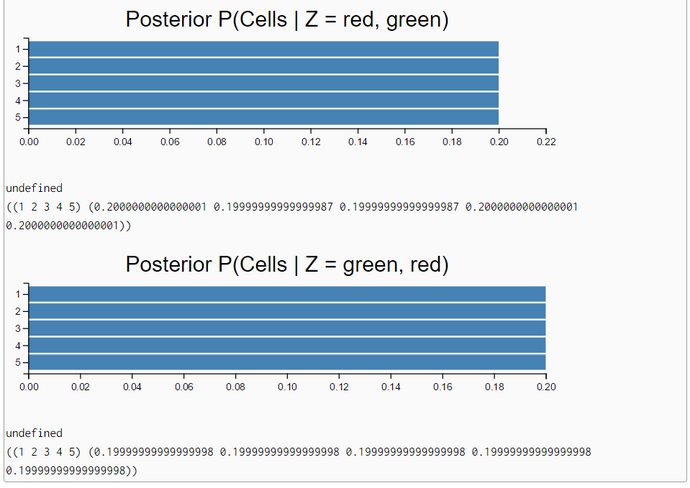
The inferences with the exact enumeration-query algorithm demonstrate very clearly that the robot "knows" rather definite that when "seeing" a color he is in the red or green subworld. If he "sees" two alternating colors without moving he is completely uncertain about his location. His belief distribution after seeing the sequence 'red, green' or vice versa is equal to the prior belief distribution.
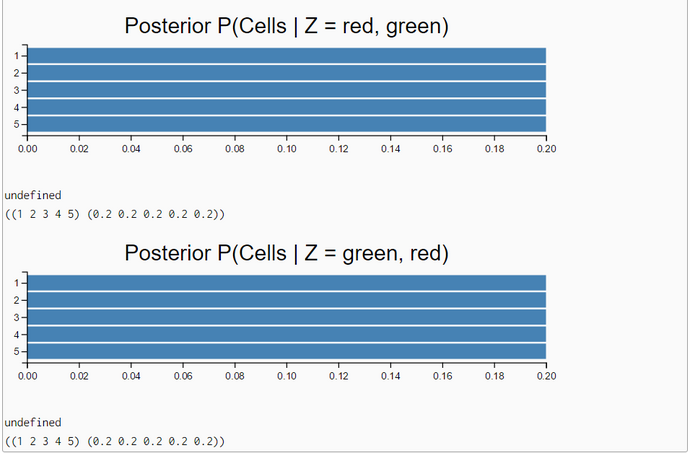
Lesson1: Localization - Measurement Update with Sense and Z = 'white' - (WebChurch: enumeration-query, function combination)
;------------------------------------------------------------------------------------------------------
; Localization: Measurement Update with Sense Function and Z = 'white'
; - WebChurch code by PCM 2016/03/04 -
; instruction by Sebastian Thrun, AI for Robotics,
; www.udacity.com/course/viewer#!/c-cs373/l-48739381/e-48692806/m-48641537)
;------------------------------------------------------------------------------------------------------
An alternative generative model could be formulated by leaving Thrun's weights pHit and pMiss unchanged but to add a third dummy measurement category Z = 'white' with an appropriate conditional probability. By this dummy category pHit and pMiss get the semantics of proper conditional probabilities, because column sums now add up to one.
| world[i] = red | world[i] = red | |
| Z = red | pHit = 0.6 | pMiss = 0.2 |
| Z = green | pMiss = 0.2 | pHit = 0.6 |
| Z = white | (1 - pHit - pMiss) = 0.2 | (1 - pMiss - pHit) = 0.2 |
| column sum | 1.0 | 1.0 |
When the bot "perceives" a white cell he is completely uncertain about his location; his posterior belief is a uniform probability distribution.
Lesson1: Localization - Measurement Update with Sense and a Sequence of Measurements - (WebChurch: enumeration-query, foldl)
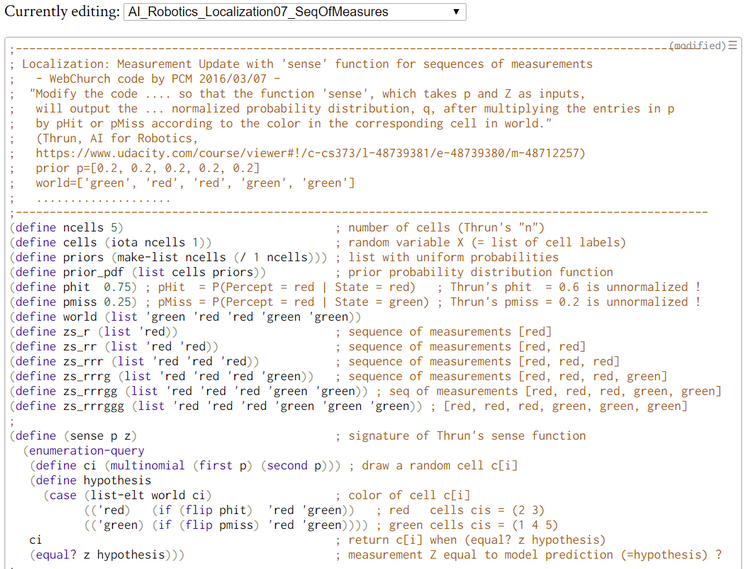
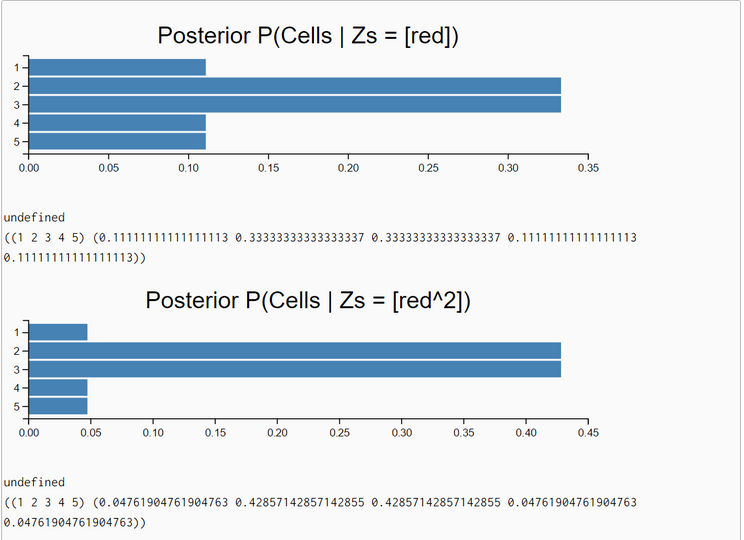
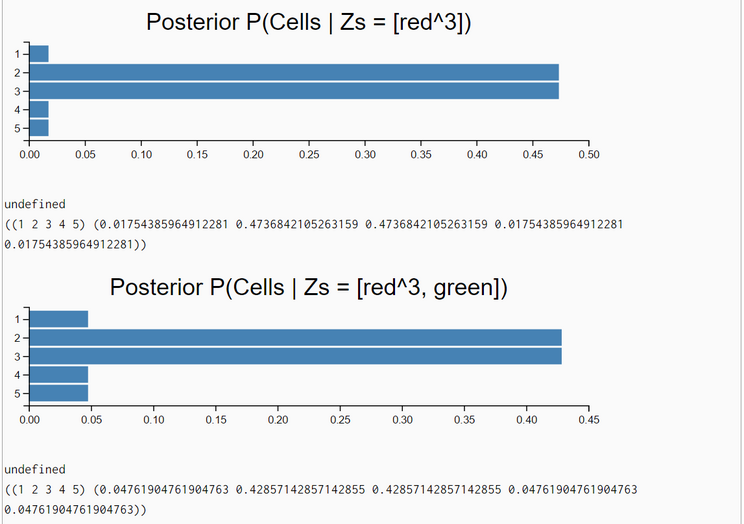
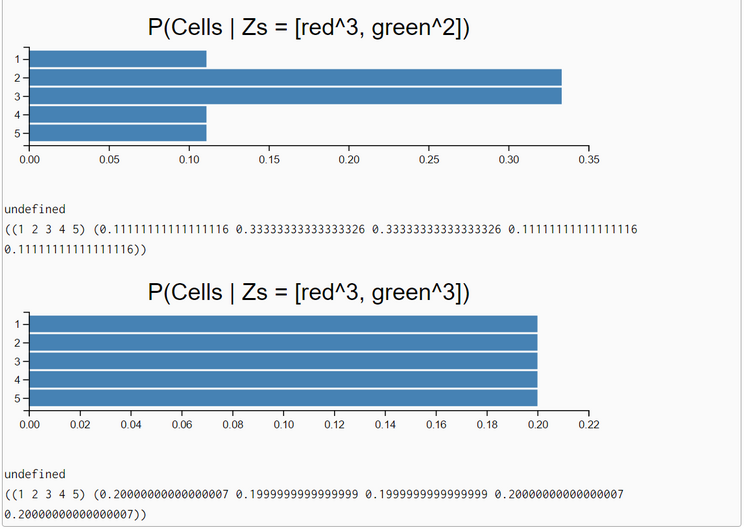
Now, the task is to do a measurement update for any sequence of measurements. Thrun uses in his Python-code a for-loop over the list of measurements. We stay in the context of pure functional programming and solve the problem elegantly with the foldl function. The progression of results demonstrate that when "seeing" repeatedly 'red' cells the confidence of being in a 'red' subworld grows. Then by "seeing" permanently 'green' cells this confidence disappears. In the end when the frequency of seeing 'red' cells is in balance with the according frequency for 'green' cells the posterior belief is equal to the prior belief distribution: the bot has no idea what is his current location.