03_Sense-Move-Cycle
03_Sense-Move-Cycle
Sense-Move-Cycle with a Sequence of two Percepts and two Moves to the Right
; - WebChurch code by PCM 2016/03/22 -
;
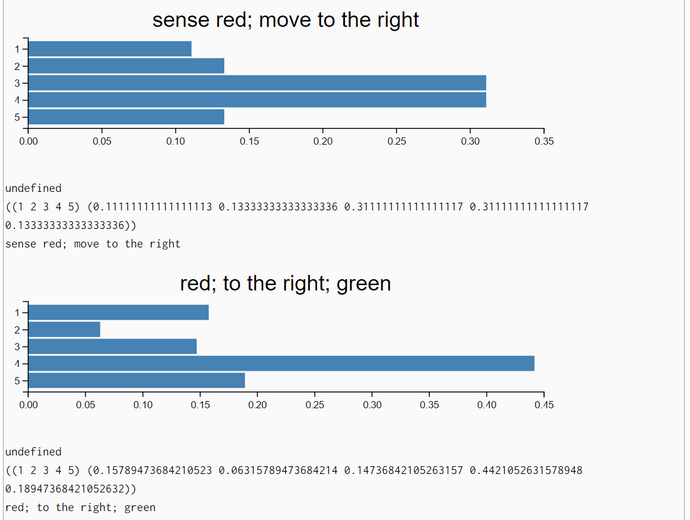
; "Given the list motions = [1,1] which means the robot moves right and then right again,
; compute the posterior distribution if the robot first senses red, then moves right one,
; then senses green, then moves right again, starting with a uniform prior distribution."
; (Thrun, AI for Robotics)
; www.udacity.com/course/viewer
;
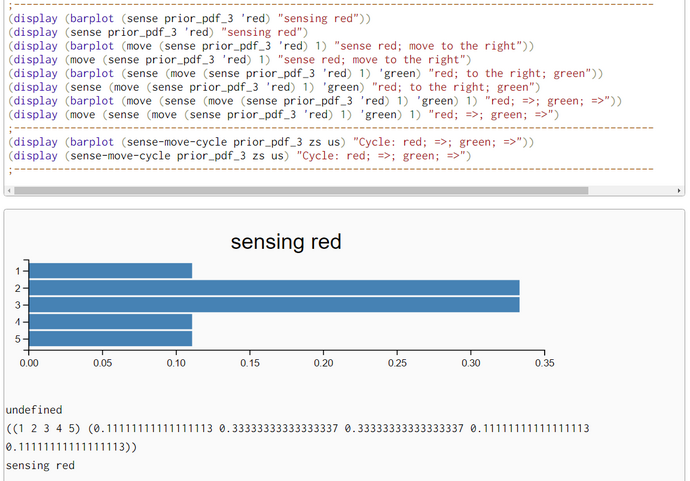
; p = [0.2, 0.2, 0.2, 0.2, 0.2]
; world = ['green', 'red', 'red', 'green', 'green']
; measurements = zs = ['red', 'green']
; motions = us = [1,1]
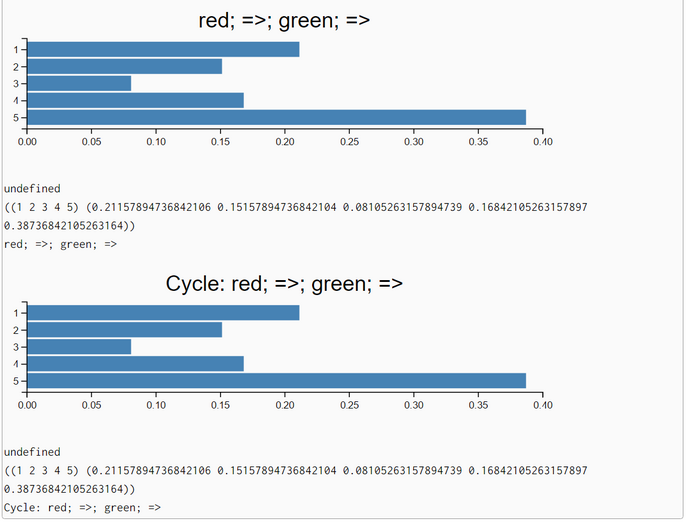
The problem is solved by humans without mathematical computations but qualitatively with the help of common sense heuristics. If the robot sees red, he should be in cell 2 or 3. After moving one step to the right, he should be in cell 3 or 4. Now, seeing green rules out the possibility of being in cell 3. So there is only one possibility left. This is cell 4. When moving from there one step to the right he icomes to rest in cell 5. We come to the same conclusion when computing the posterior pdf. The posterior belief of being in cell 5 is p = 0.387 and higher than the belief of being in other cells.

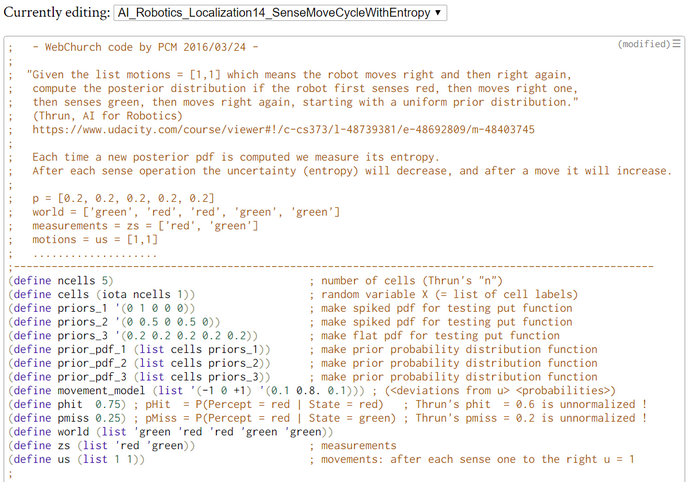
Sense-Move-Cycle with Entropy Measurement
; - WebChurch code by PCM 2016/03/23 -
;
; "Given the list motions = [1,1] which means the robot moves right and then right again,
; compute the posterior distribution if the robot first senses red, then moves right one,
; then senses green, then moves right again, starting with a uniform prior distribution."
; (Thrun, AI for Robotics)
; www.udacity.com/course/viewer
;
; Each time a new posterior pdf is computed we measure its entropy
;
; p = [0.2, 0.2, 0.2, 0.2, 0.2]
; world = ['green', 'red', 'red', 'green', 'green']
; measurements = zs = ['red', 'green']
; motions = us = [1,1]
; ....................
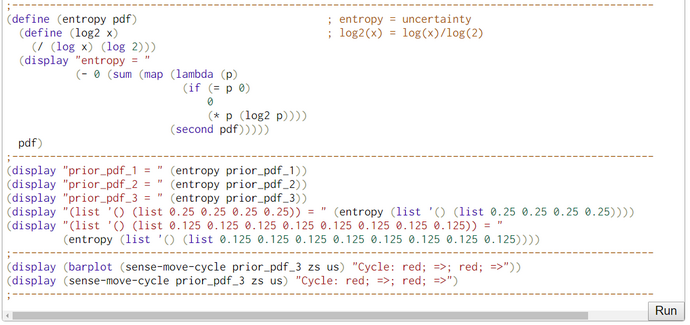
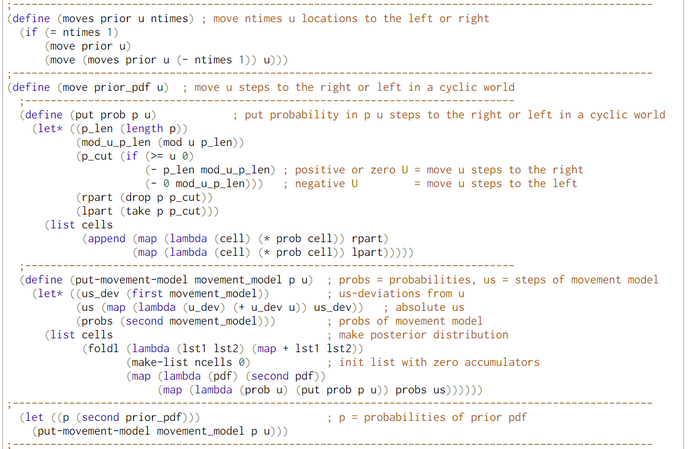
Each perception with sense reduces the uncertainty (= entropy) of belief in locations. The reverse is true after each movement. Each move increases the bots's uncertainty (= entropy) concerning his location. This up and down can be observed in our entropy computations.

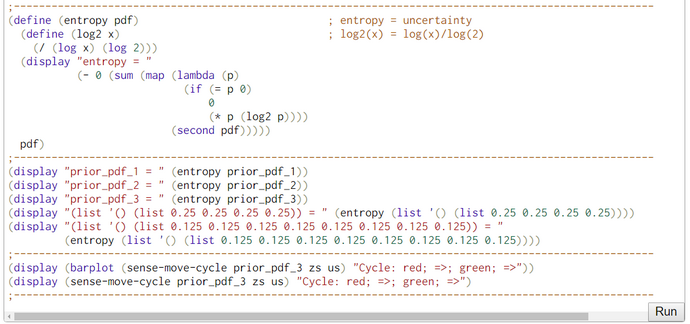

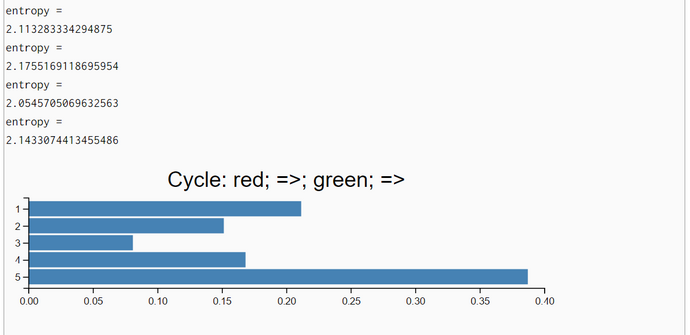
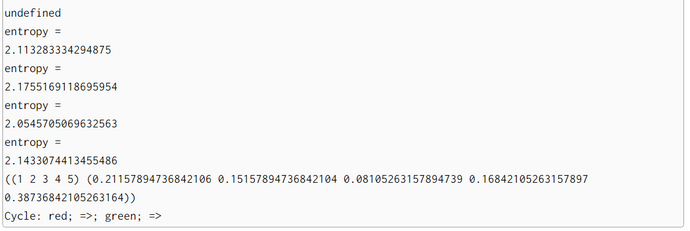
Sense-Move-Cycle: Sense(Red) => Move(Right 1) => Sense(Red) => Move(Right 1)
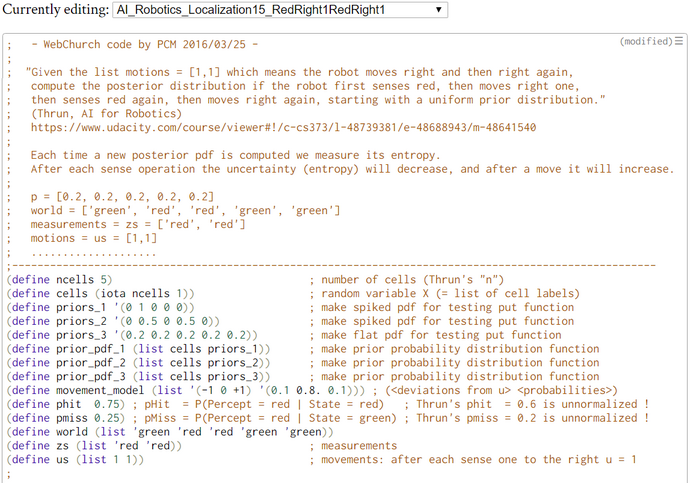
; - WebChurch code by PCM 2016/03/25 -
;
; "Given the list motions = [1,1] which means the robot moves right and then right again,
; compute the posterior distribution if the robot first senses red, then moves right one,
; then senses red again, then moves right again, starting with a uniform prior distribution."
; (Thrun, AI for Robotics)
; www.udacity.com/course/viewer
;
; p = [0.2, 0.2, 0.2, 0.2, 0.2]
; world = ['green', 'red', 'red', 'green', 'green']
; measurements = zs = ['red', 'red']
; motions = us = [1,1]
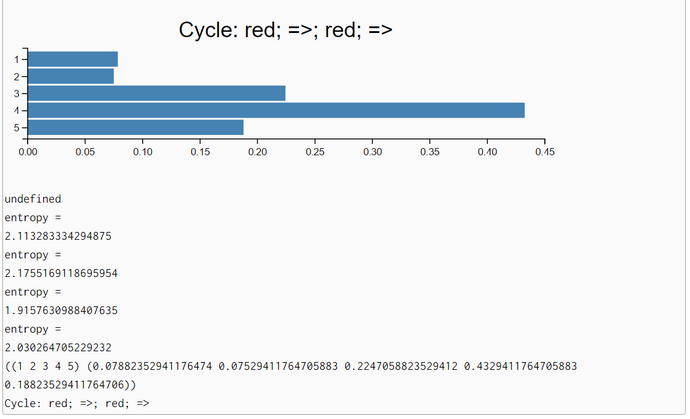
The problem is solved by humans without mathematical computations but qualitatively with the help of common sense heuristics. If the robot sees red, he should be in cell 2 or 3. After moving one step to the right, he should be in cell 3 or 4. Now, seeing red again rules out the possibility of being in cell 4. So there is only one possibility left. This is cell 3. When moving from there one step to the right he comes to rest in cell 4. We come to the same conclusion when computing the posterior pdf. The posterior belief of being in cell 4 is p = 0.43294 and higher than the belief of being in other cells.