1. Background and Motivation

Inspector Clouseau is a well-known fictitious figure. Despite his at first glance incompetence, he solves his cases through lucky coincidences and intuition. The latter he has acquired through many years of professional experience. Although many academic psychologists doubt that a human is able to draw conclusions according to Bayesian rules, we use this example to demonstrate some basic aspects of modeling, coding and calculation.

2. Scenario

David Barber describes the the scenario as: Inspector Clouseau arrives at the scene of a crime. The victim lies dead in the room alongside the possible murder weapon, a knife.  The Butler (B) and Maid (M) are the inspector’s
main suspects and the inspector has a prior belief of 0.6 that the Butler is the murderer, and a prior belief
of 0.2 that the Maid is the murderer.  These beliefs are independent in the sense that p(B,M) = p(B)p(M).
(It is possible that both the Butler and the Maid murdered the victim or neither). (D.Barber, 2012, 2016)

3. Modelling Approach

We follow a multi-level modeling process. Step 1: DAG of the probabilistic graphical model, Step 2: Decoration of the DAG with numerical parameters, Step 3: Mathematical Specification, Step 4: Coding of the generative probabilistic graphical model in WebPPL, Step 5: Comparison of the results of this step with those from Step 3.

3.1. Modelling Step: DAG of Generative Probabilistic Model

The direct acyclic graph (DAG) should be modelled along the causal directions of influence (Fig. 1): The possible actors (persons) can trigger actions and cause effects (e.g. murder). There are two possible actors (e.g. the butler and the housemaid) who can perform actions (e.g. kick with a knife). The actors are modelled by two nodes. Furthermore, there is an object (knife) with two uncertain roles: either it was used for the murder or not. The knife is also modeled by a node. The use of the object depends on the roles of both actors. So the object node gets two incoming arrows with the actor nodes as sources. Since there are no indications of external or exogenous influences, the actor nodes receive no incoming arrows. Inspector Clouseau also believes that the possible actors are independent of each other, so there are no connection arrows between them. The DAG has a V-structure. In the scientific literature this is referred to as "collider" (Barber, 2012, 2016; Pearl et al, 2016).

3.2. Modelling Step: Decoration of DAG with Numerical Parameters

The parameters (absolute and conditional probabilities) of the model can be found in Barber's book (Barber, 2012, p.9f; 2016). They reflect the beliefs of Inspector Clouseau as he enters the scene. According to the findings of psychology and behavioural economics, probabilities cannot be obtained directly from interviews. They can only be obtained indirectly through betting or other experimental arrangements (e.g. wheels of fortune). We assume that David Barber successfully sketched out Inspector Clouseau's attitudes precisely in the form of probabilities.
The DAG is equipped with all the necessary un- and conditional probabilities (Fig. 1).

Modelling Step 3.3: Mathematical Specification

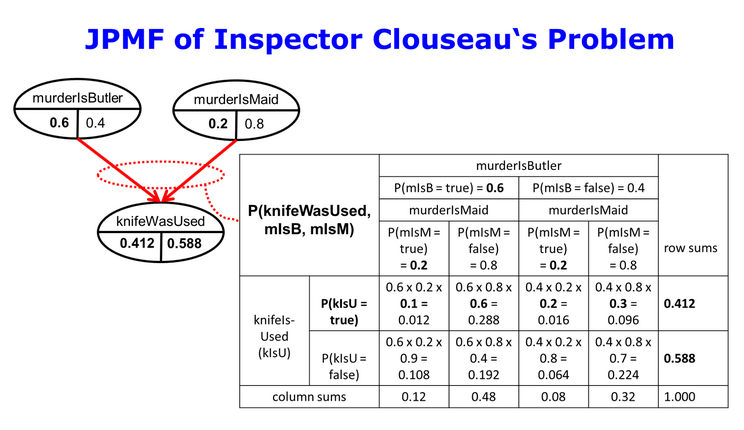
3.3.1 Joint Probability Mass Function (JPMF) 'Inspector Clouseau'

Barber gives a hint that the JPMF (Pishro-Nik, 2014, 2019) should be

$$ P(K, B, M) = P(K | B, M) * P(B, M) = P(K | B, M) \cdot P(B) \cdot P(M) $$

This is exactly the mathematical semantics of the DAG in Figure 1. The JPMF can be found in Figure 2. The computations for the JPMF in Fig 2  are specified by the formula above.

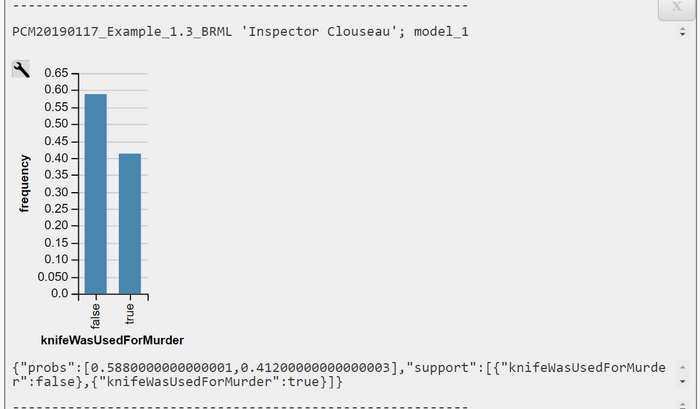
3.3.2 Prior Belief about the Marginal PMF P(K) = P(knifeWasUsedForMurder)

The prior belief about the knife as a crime weapon is

$$ P(K) = \sum_{B, M} P(K, B, M) = \sum_{B, M} P(K | B, M) \cdot P(B) \cdot P(M) $$

$$ = \sum_{B} P(B) \sum_{M} P(K | B, M) \cdot P(M) = \langle P(K=true) = \textbf{0.412}, P(K=false) = 0.588\rangle$$

Thus Inspector Clouseau is rather uncertain about the role of the knife.

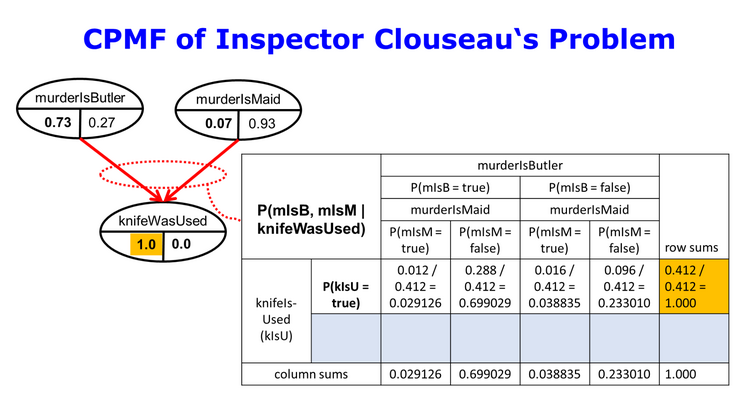
3.3.3 Modelling Step:  Inferences P(... | K = true)

Under the hypothesis that the knife was used in the murder the posterior belief about their joint killer roles is the conditional probability

$$ P(B, M | K) = \frac{P(K | B, M) \cdot P(B) \cdot P(M)} {P(K)} $$

The posterior belief that both Butler and Maid conspired to commit murder is rather low

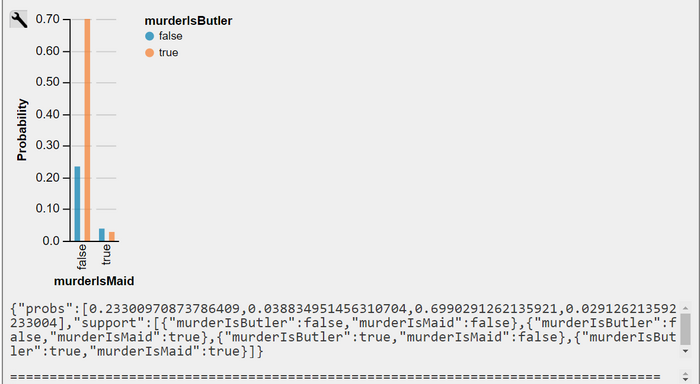
$$P(B=true, M=true | K=true) = \textbf{0.029126}$$

This information can be obtained by a look up in Fig 2 or in the Output_3-model_2.

The posterior beliefs about a single actor under the same hypothesis are

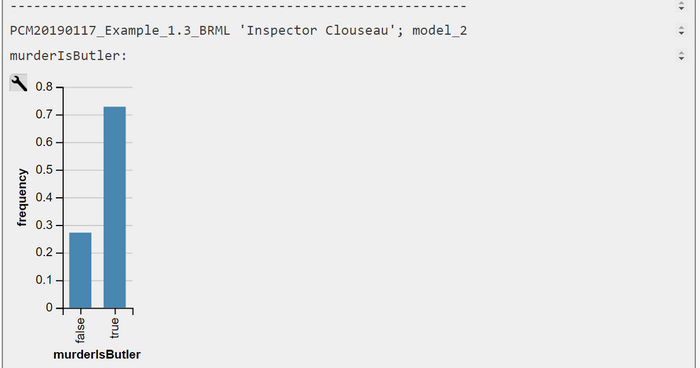
$$ P(B | K) = \frac{P(B) \cdot \sum_{M} P(K | B, M) \cdot P(M)} {P(K)} = \textbf{0.728}$$

and

$$ P(M | K) = \frac{P(M) \cdot \sum_{B} P(K | B, M) \cdot P(B)} {P(K)} = \textbf{0.068}$$