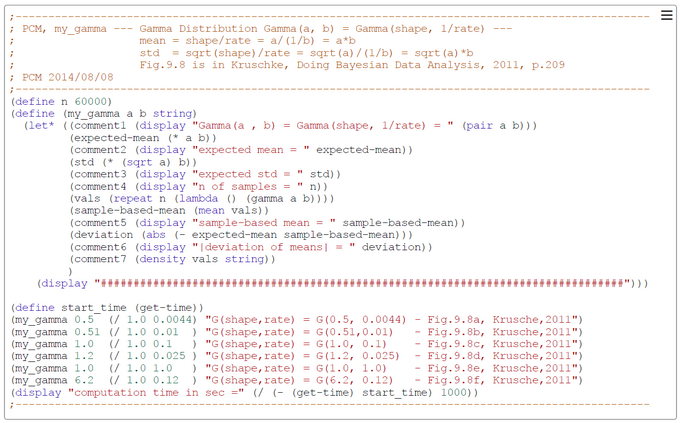
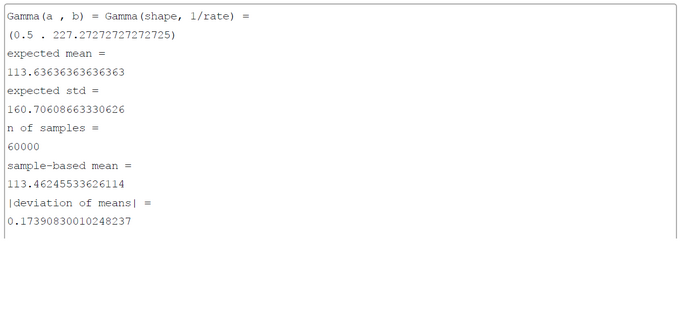
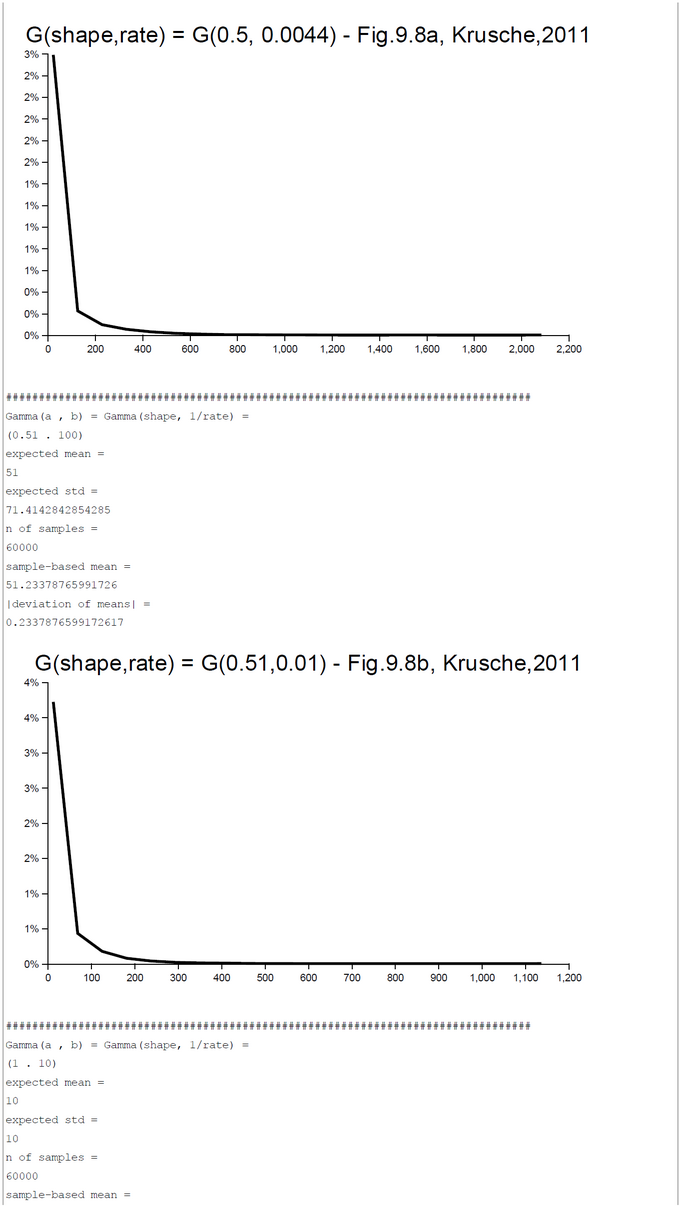
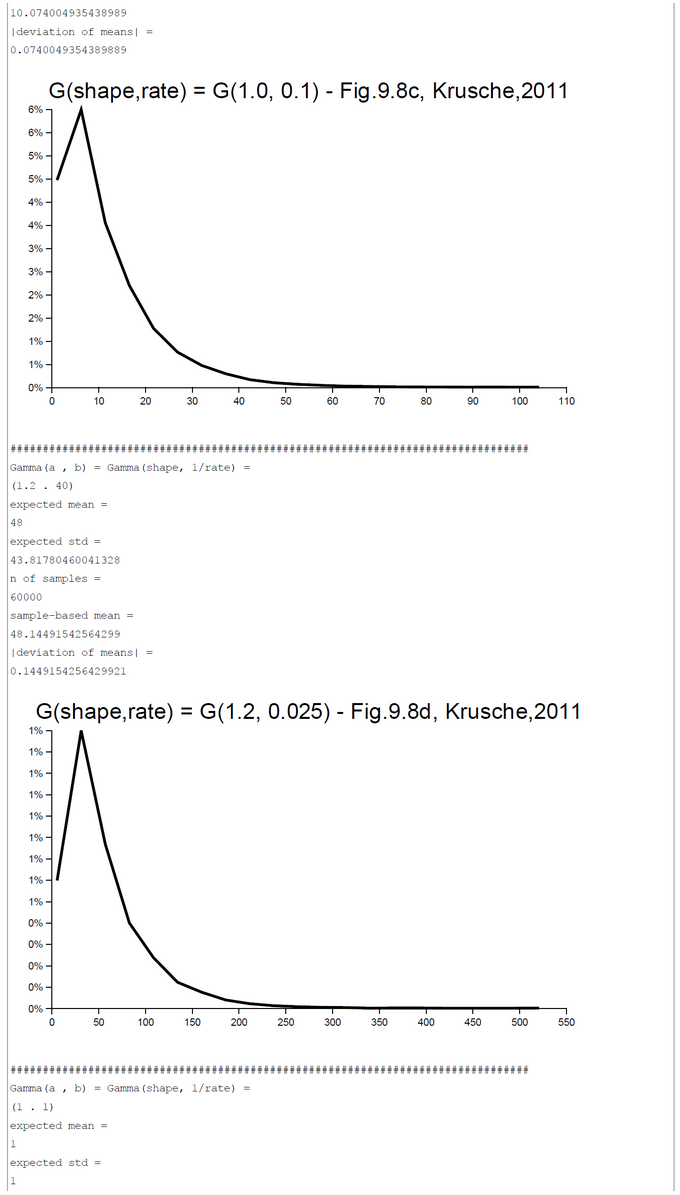
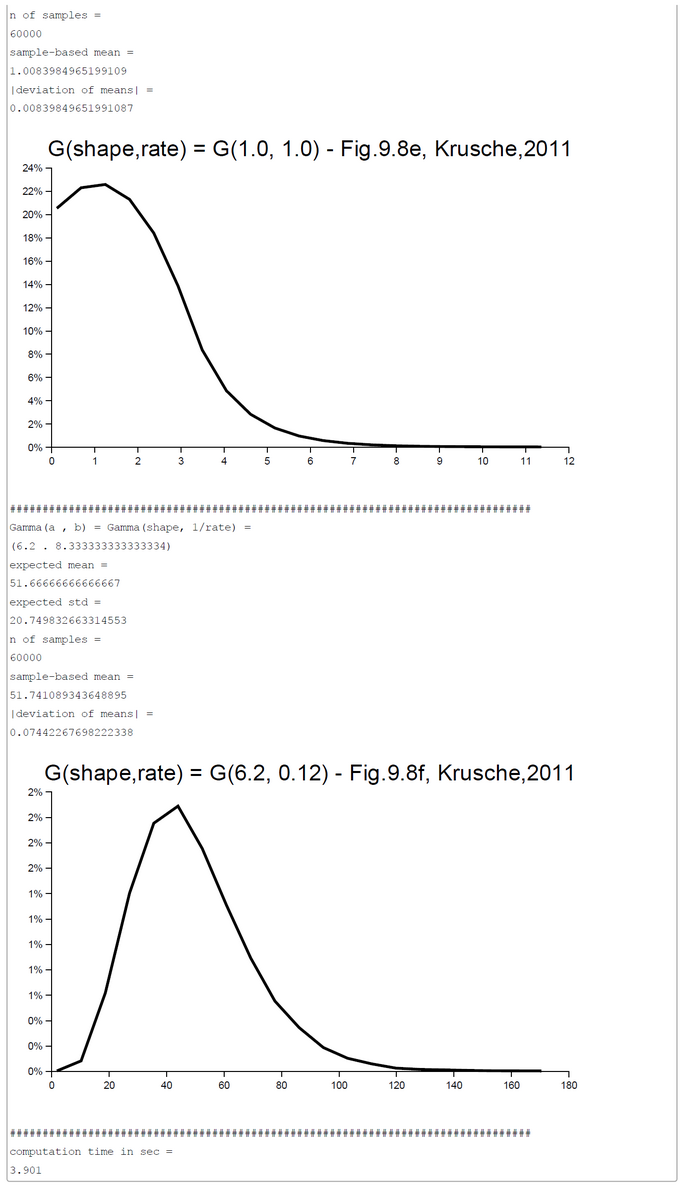
Appendix 1: Gamma-Distribution
Appendix 1: Gamma-Distribution
Appendix 1: The Gamma-Distribution
"Gamma distributions are used as sampling distributions for positive and skewed data, such as costs or times to events... Note that the gamma is sometimes parameterised in terms of the scale 1/b instead of the rate b." (LUNN et al., The BUGS Book, 2013, p.345f). In OpenBUGS the b-parameter is from type scale and in WebCHURCH it is from type rate.
When developing a Bayesian model most often a and b are unknown but instead we have some vague idea about the mean and variance of the gamma-distributed priors. So we need equations for a and b in terms of the mean and variance of the gamma-distributed variable. In the table below is a summary of the relations between the parameters.
| OpenBUGS | WebCHURCH | |
|---|---|---|
| expression in programming language | X ~ dgamma(a, b) | (define x (gamma a b)) |
| mean m | E(X) = m = a/b | E(X) = m = a*b |
| variance s^2 | Var(X) = s^2 = a/(b^2) | Var(X) = s^2 = a*(b^2) |
| standard deviation s | Std(X) = s = sqrt(a)/b | Std(X) = s = sqrt(a)*b |
| shape parameter a | a = (m^2)/(s^2) | a = (m^2)/(s^2) |
| scale or rate parameter b | b = m/(s^2) ## scale | b = (s^2)/m ;; rate |
Below are the derivations of a and b in terms of m and s for OpenBUGS and WebCHURCH.
| OpenBUGS | WebCHURCH | |
|---|---|---|
| shape parameter a | a/b = m ==> a = m*b ==> a = m*(sqrt(a)/s) ==> (a/sqrt(a)) = (m/s) ==> sqrt(a) = m/s ==> a = (m^2)/(s^2) | a = m/b ==> a = m *(1/(s/sqrt(a))) ==> a = m*(sqrt(a)/s) ==> a/sqrt(a) = m/s ==> a = (m^2)/(s^2) |
| scale/rate parameter b | sqrt(a)/b = s ==> sqrt(a)/s = b ==> (m/s)/s = b ==> (m/s)*(1/s) = b ==> b = m/(s^2) ## scale | b = s/sqrt(a) ==> b = s/(m/s) ==> b = s*(s/m) ==> b = (s^2)/m ;; rate |
Appendix 1: Use of Gamma-Distribution in CHURCH
The CHURCH-code can be found here.