Hoeffding Bound
Hoeffding Bound
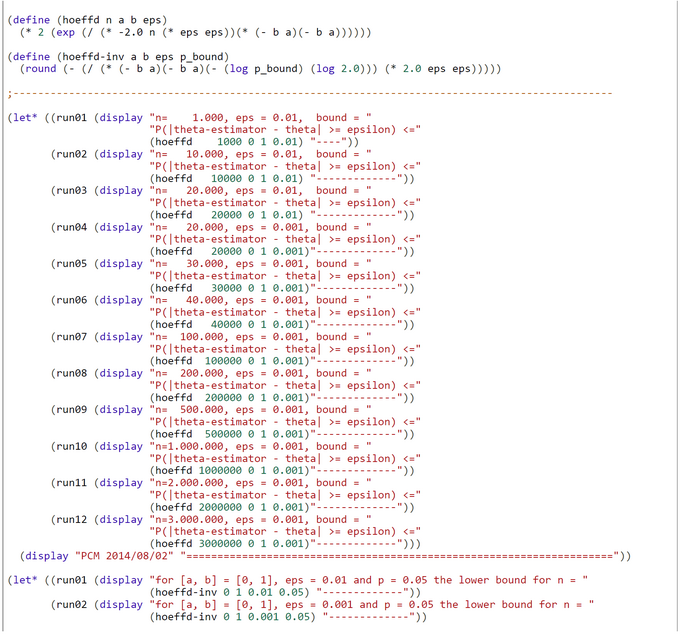
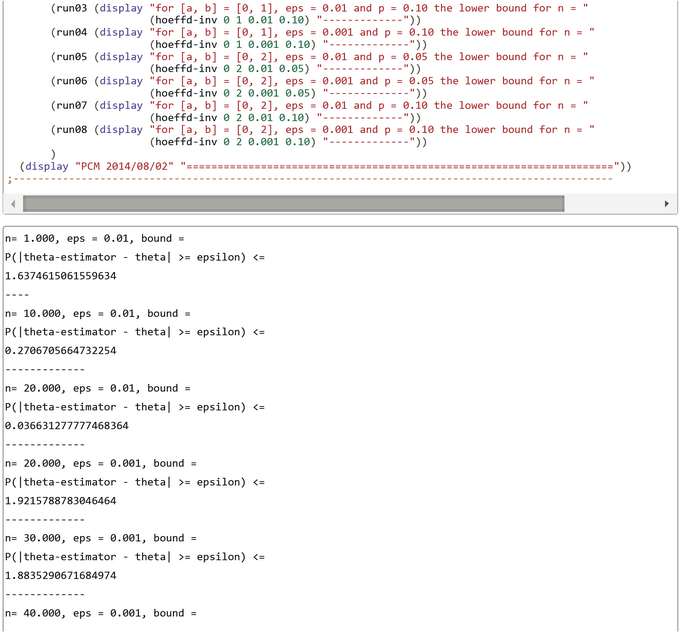
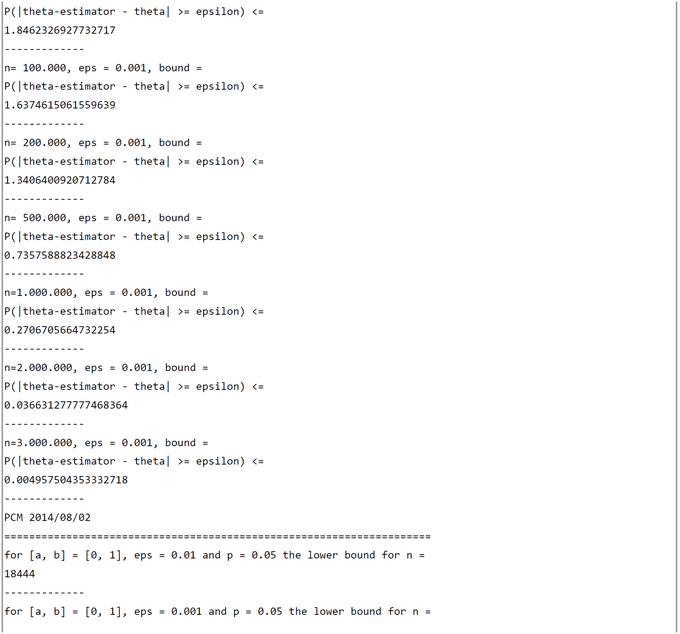
CHURCH-Code for Hoeffding Bound: Minimal Sample Size n
In many of our simulations where we estimate a parameter theta we are interested in the probability that the sample-based estimator theta-bar is close to theta for a concrete choice of sample-size n. The Hoeffding bound measures errors in terms of the absolute distance |theta-bar - theta|. "The bound asserts that, with very high probability, theta-bar is within an error epsilon of the true probability theta. The probability is taken relative to possible data sets D. ...The bound tells us that, for most data sets D that we gerate at random, we obtain a good estimate. Furthermore, the fraction of "bad" sample sets D, those for which the estimate is more than epsilon from the true value, diminishes exponentially as the number of samples n grows." (Koller & Friedman, 2009, A.2.2, p.1145)
The Koller & Friedman formulas are 'one-sided' because the bounds are sensitive to the direction of the deviation, whereas Murphy (Murphy, 2012, (6.67), p.209) presents a 'two-sided' version. Dümbgen (Dümbgen, Stochastik für Informatik, Springer, 2003, Ch.7.4, p.125, ISBN 3-540-00061-5) presents a generalization of the formula used by Murphy. The variables are not constrained to the interval [0, 1].
The Church program is a translation of Dümbgens formula. But more valuable than the Hoeffding bound is the required minimal sample-size n for a given epsilon and a given Hoeffding bound. We compute n by the function 'hoeffding-inv'.
The results are interesting. For i.i.d. Bernouill variables and for practical purposes resonable eps = 0.01 and two-sided Hoeffding bound p-bound = 0.10 the required n is n >= 14979. If we want a greater precision eps = 0.001 with same p-bound = 0.10 we have to increase the sample size to n >= 1.497.866 !