Mixture Model for the 'Seven Scientists' Problem
Mixture Model for the 'Seven Scientists' Problem
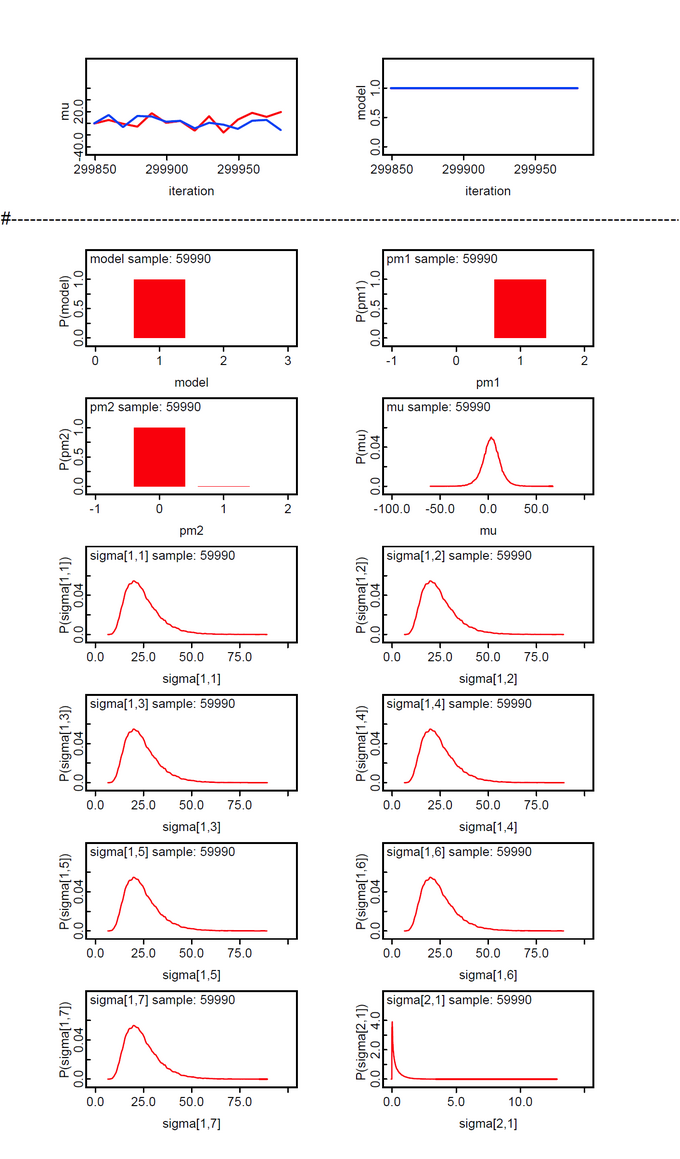
OpenBUGS Model 1: Single-Sigma Model
When experimenting with different Gamma-hyperparameters a and b for the individual prior noise level sigma we found in our WebCHURCH program that for hyperparameters a=b=7 all posterior individual noise levels had nearly the same standard deviation sd. As OpenBUGS is more abstract than WebCHURCH we prefer to construct the mixed model for the Seven Scientist problem first in the OpenBUGS modelling language.
Here we present the single-sigma OpenBUGS model for the WebCHURCH parametrization (gamma 7.0 7.0). Because the hyperparameter b in WebCHURCH is equal to its inverse the parametrization in OpenBUGS is b = 1/7 = 0.142857 and dgamma(7.0, 0.142857).
OpenBUGS code and simulation results are presented below. A comparison with the corresponding WebCHURCH model demonstrates that the posterior parmeters are nearly identical.
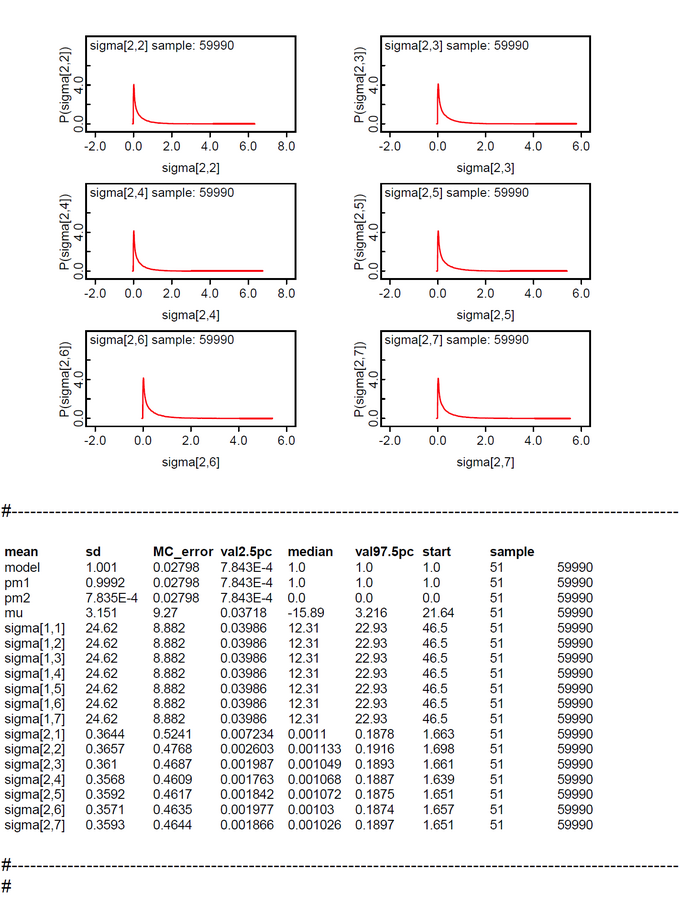
OpenBUGS Model 2: Multiple-Sigma Model
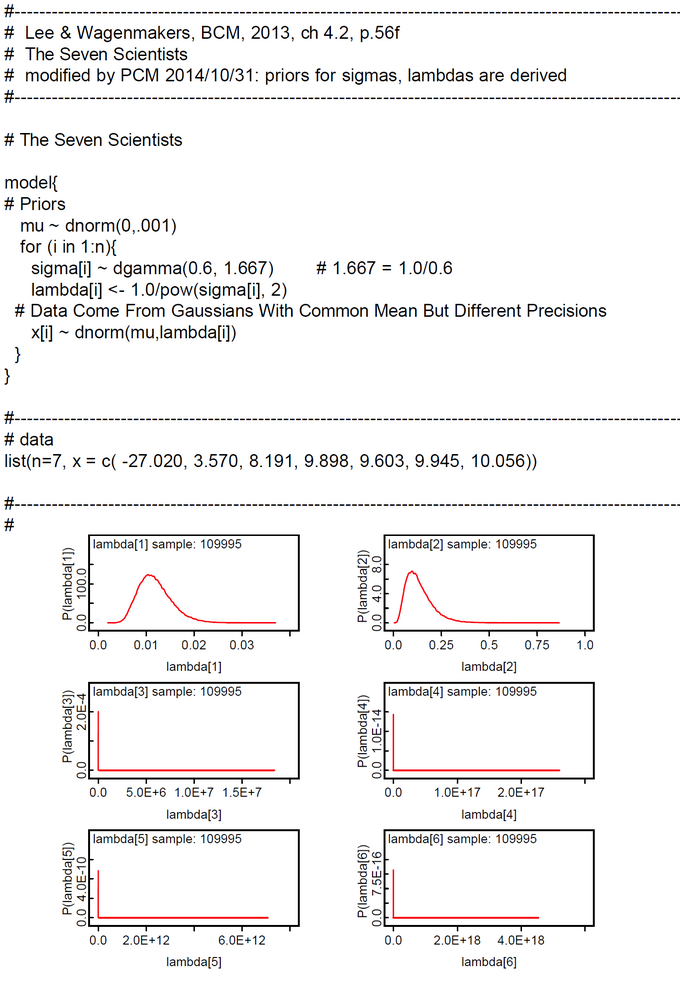
When experimenting with different Gamma-hyperparameters a and b for the individual prior noise level sigma we found in our WebCHURCH program that for hyperparameters a=b=0.6 all posterior individual noise levels had the greatest range of individual range of standard deviations sd. As OpenBUGS is more abstract than WebCHURCH we prefer to construct the mixed model for the Seven Scientist problem first in the OpenBUGS modelling language.
Here we present the multiple-sigma OpenBUGS model for the WebCHURCH parametrization (gamma 0.6 0.6). Because the hyperparameter b in WebCHURCH is equal to its inverse the parametrization in OpenBUGS is b = 1/0.6 = 1.6667 and dgamma(0.6, 1.6667).
OpenBUGS code and simulation results are presented below. A comparison with the corresponding WebCHURCH model demonstrates that the posterior parameters are very comparable. Only sigma[1] in OpenBUGS ist nearly 30% greater than in the WebCHURCH run.
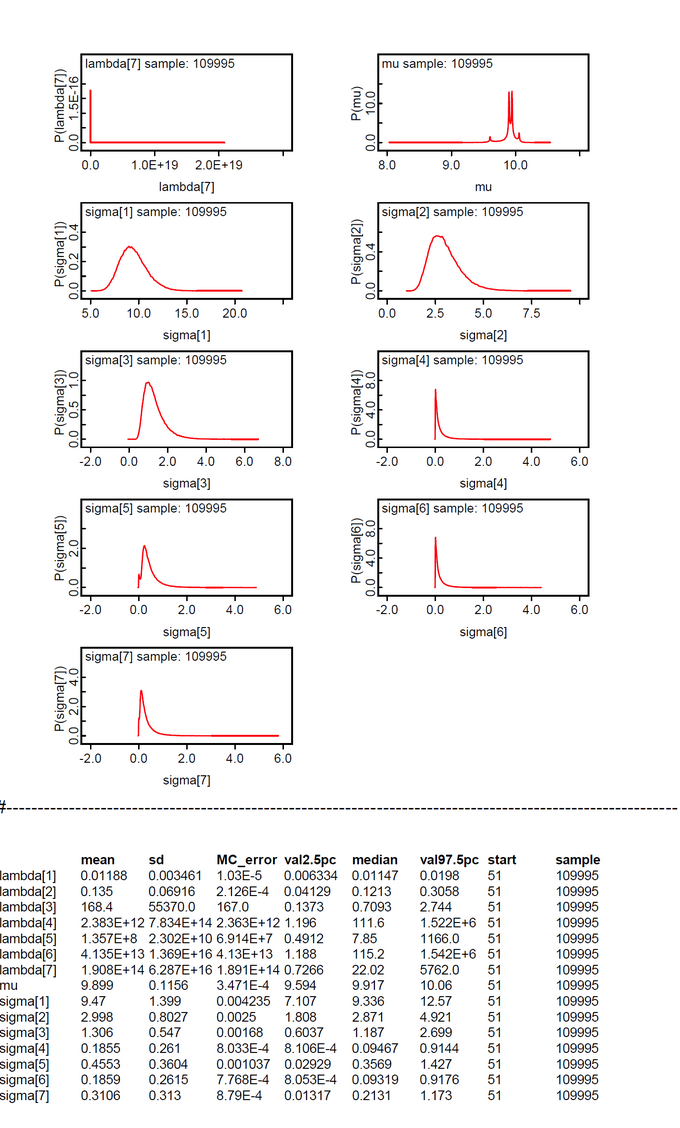
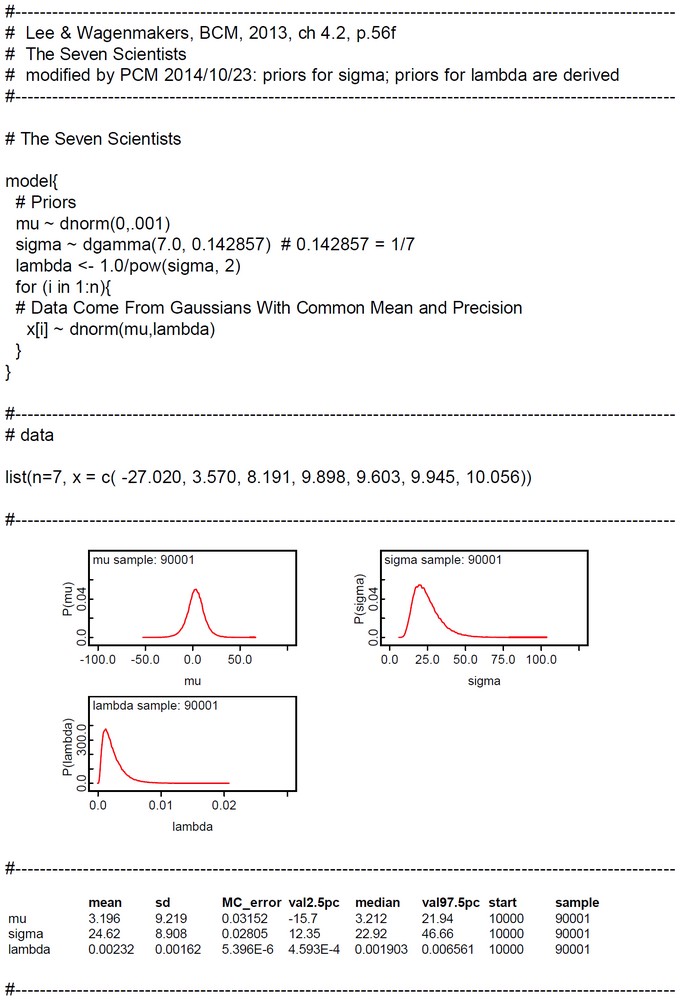
OpenBUGS Model 3: The Mixture Model for the 'Seven Scientists' Problem
We modeled the model check as a mixture model with two submodels: Model 1 'Single-Sigma' Model and Model 2 'Multiple-Sigma' Model. Our code is an implementation of the Bayes Factor test (Lunn et al., 2013, p.169). The priors for the two models are p(theta[1]) = p(theta[1]) = 0.5. So the prior Bayes Factor is 1.It is recommended "that Bayes factors require informative prior distributions under each model." (Lunn et al., The BUGS Book, 2013, p. 169) We think that our priors comply with this recommendation.
We ran the code with two Markov chains starting with different initials for mu. The initials for the sigma were generated automatically. The posterior Bayes Factor P(Model1 | data) / P(Model2 | data) = pm1/pm2 = 0.9992/0.000785 = 1272.866 shows "decisive" evidence in favor of Model 1 'Single-Sigma' Model. The qualification "decisive" was taken from the 'calibration' table 8.4 of the BUGS book (Lunn et al., 2013, p.170). This is not very astonishing as the 'Multiple-Sigma' Model is overparametrized and underconstrained. It contains even more parameters as observations! This is a severe flaw of the Lee & Wagenmakers proposal.