Example 6c: Bayesian Network 'Student Model' with further evidence
Example 6c: Bayesian Network 'Student Model' with further evidence
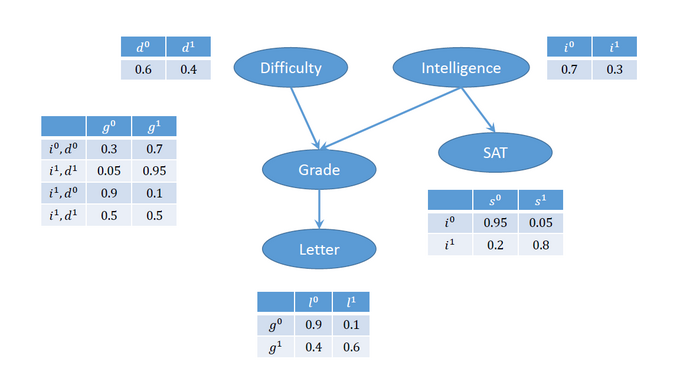
DAG of Bayesian Network 'Student Model'
Andrew D. Gordon, Thomas A. Henzinger, Aditya V. Nori, and Sriram K. Rajamani. 2014. Probabilistic programming. In Proceedings of the on Future of Software Engineering (FOSE 2014). ACM, New York, NY, USA, 167-181. DOI=10.1145/2593882.2593900 doi.acm.org/10.1145/2593882.2593900
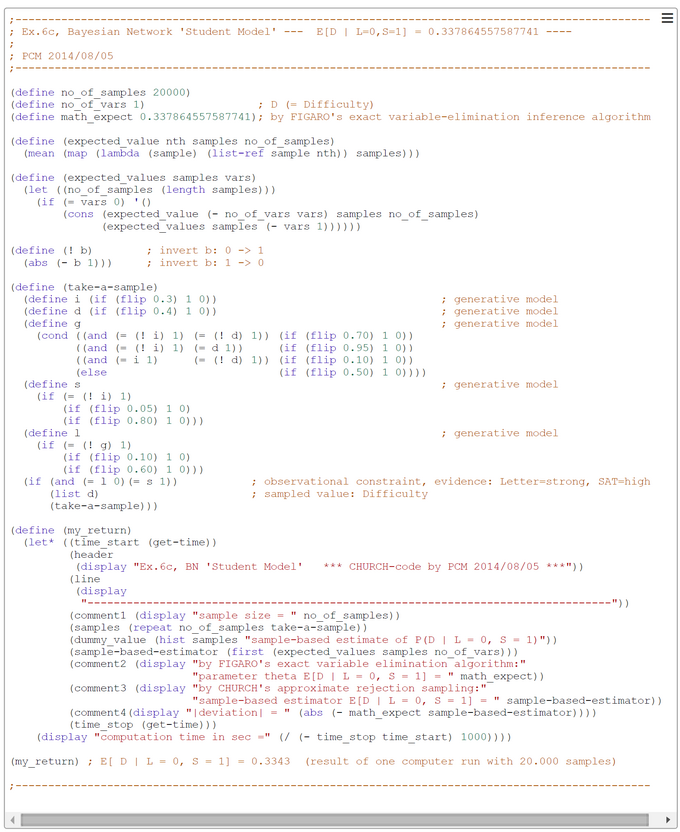
Ex6c: CHURCH-Code for Bayesian Network 'Student Model' and Inference P(D | L=0, S=1)
The generative model of the functional CHURCH program is contained in the CHURCH function "take-a-sample". The direction of inference in the conditional P[D | L=0, S=1) = P(Difficulty | strong_letter, SAT=high) is inverse to the direction of CPDs in the generative Bayesian network.
Here is a summary of the domains due to the modifications of Gordon et al. (2014):
Val(D) = <d0, d1> = <easy, hard>
Val(I) = <i0, i1> = <non smart, smart>
Val(G) = <g0, g1> = <A, B+C> = <excellent, good+average>
Val(S) = <s0, s1> = <low score, high score>
Val(L) = <l0, l1> = <strong_letter, weak_letter>
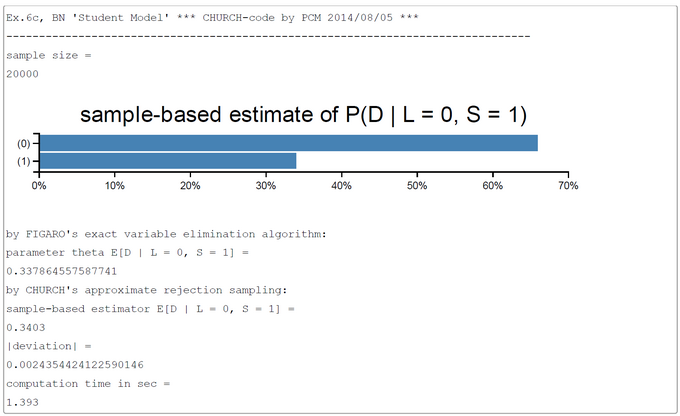
The number of samples was set to 20000 in this run. This number could in principle be increased to get a better precision of estimates. The value of the variable math_expect (= parameter theta in the HOEFFDING inequality) was computed by the exact 'variable-elimination' inference method in the probabilistic programming language FIGARO. The sampling method used in our CHURCH-program is the simple-to-understand 'forward sampling'. The screen-shot presented was generated by using the PlaySpace environment of WebCHURCH.
The inferred E(D | L=0, S=1) = P(D=1 | L=0, S=1) is near 0.34 and lower than its unconditional counterparts E(D) = P(D=1) = 0.40. So the verbal interpretation is "If you have a strong recommendation letter and an above average SAT score, then the course is more easy for you than for the average student".