Mixture Models of pairs of Binomial Models
Mixture Models of pairs of Binomial Models
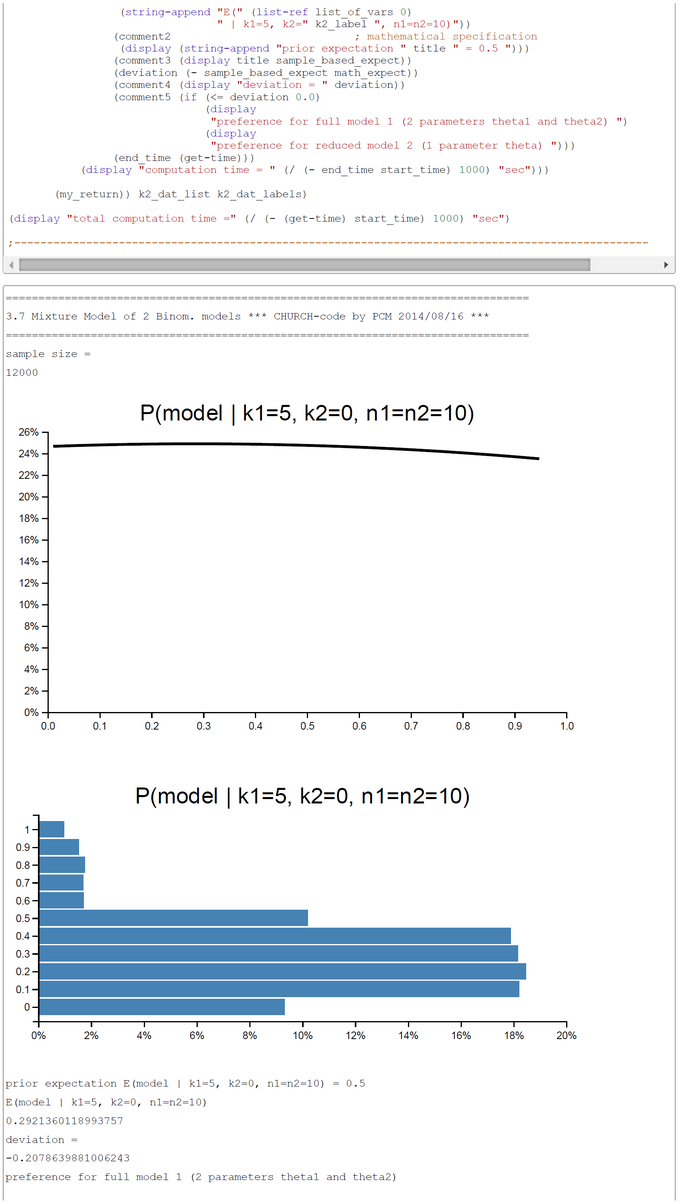
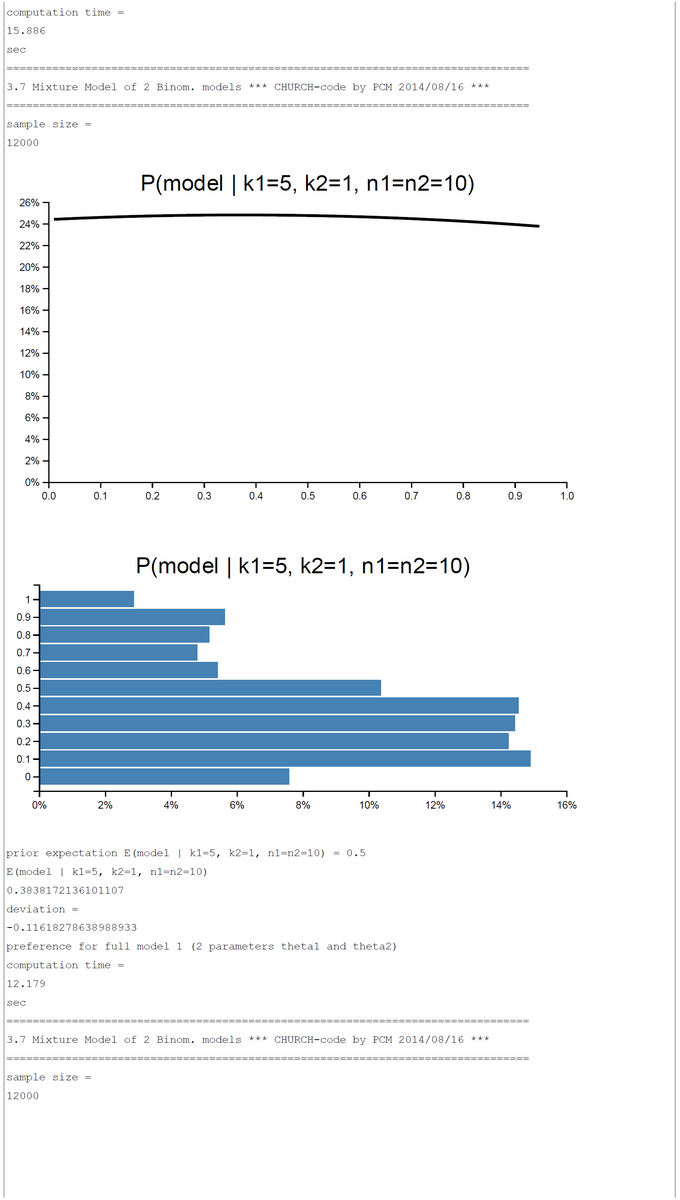
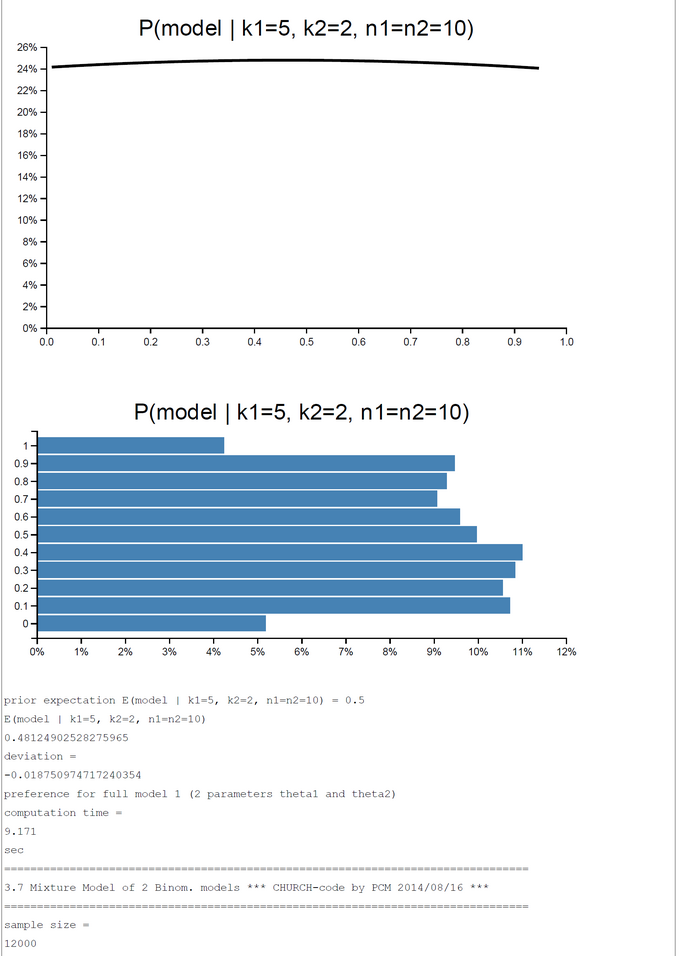
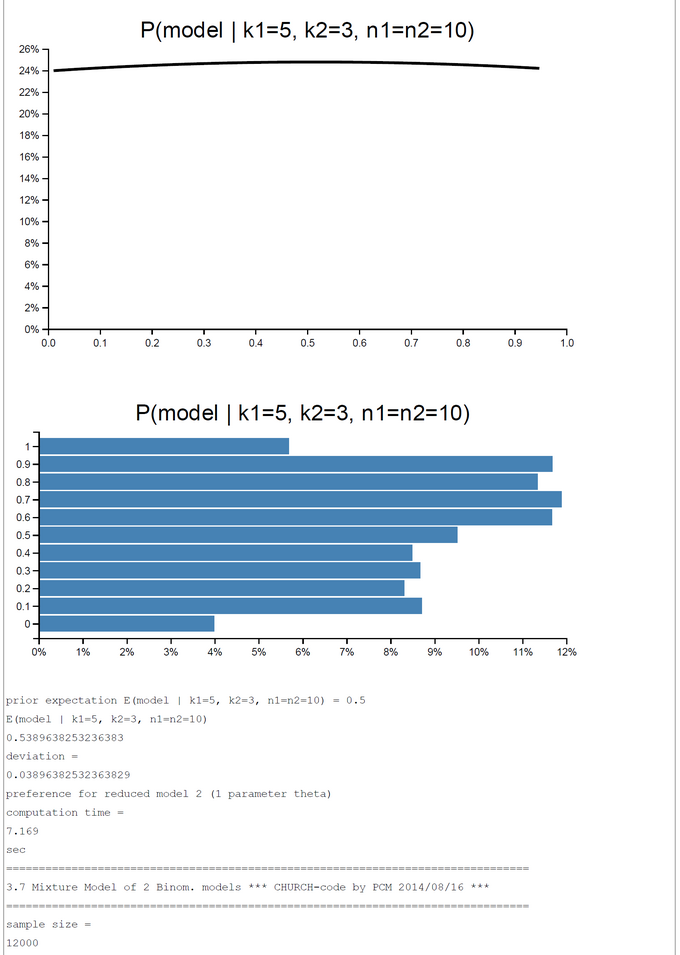
CHURCH-Code - Mixture Model of Two Binomial Models - k1=5; k2=0,...,10; n1=n2=10
We have two alternative hypotheses concerning the causal process of generating two sets of successes out of n1 and n trials:
Hypothesis 1: There a two processes with rates theta1 and theta2 generating k1 and k2 successes out of n1 and n2 trials. The hypothesis is represented by the 'full' model 1.
Hypothesis 2: There is one process with common rate theta generating k1 and k2 successes out of n1 and n2 trials. The hypothesis is represented by the 'restricted' model 2.
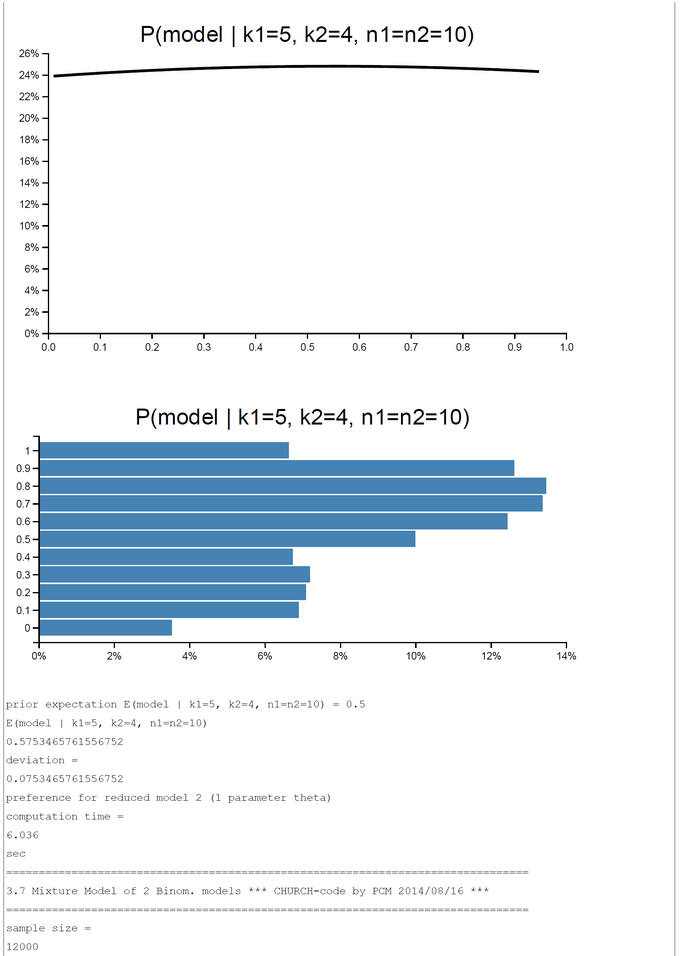
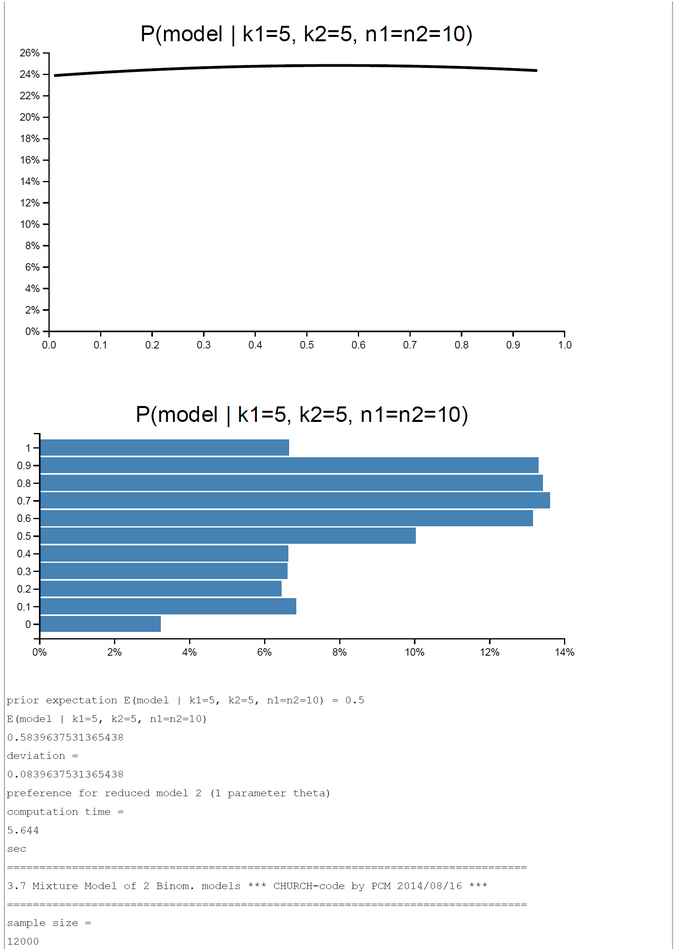
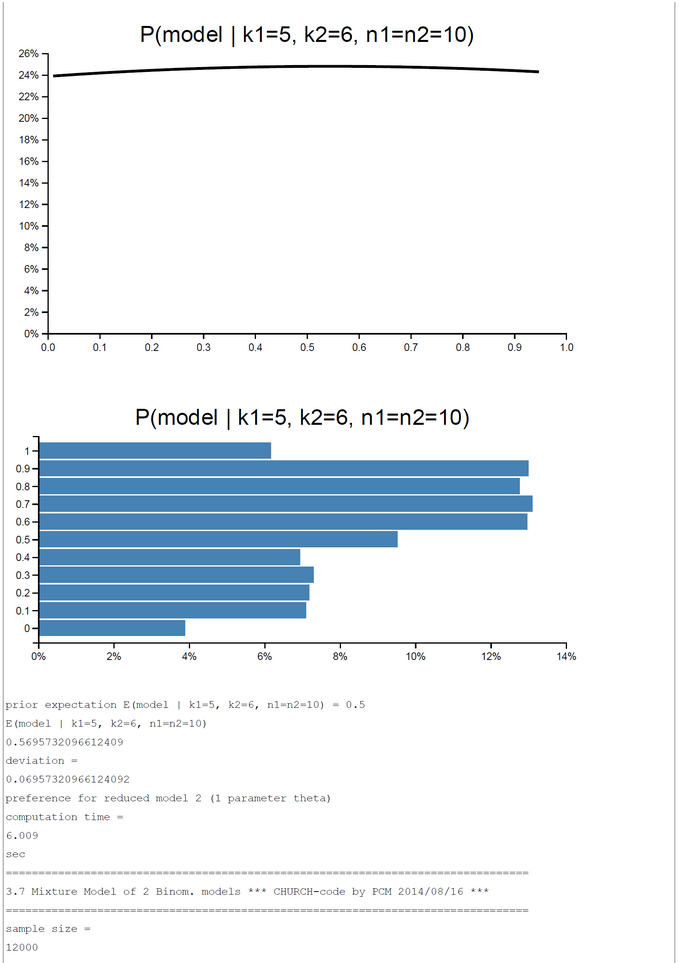
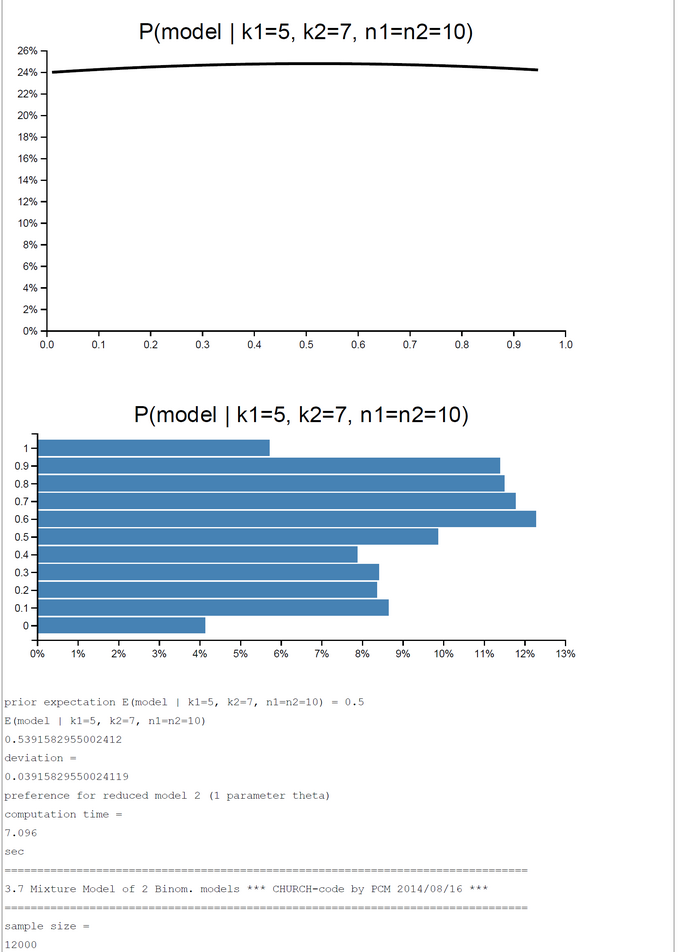
We combine both models to a mixture model. The prior probability for each of the two submodels is P(Model) = 0.5.
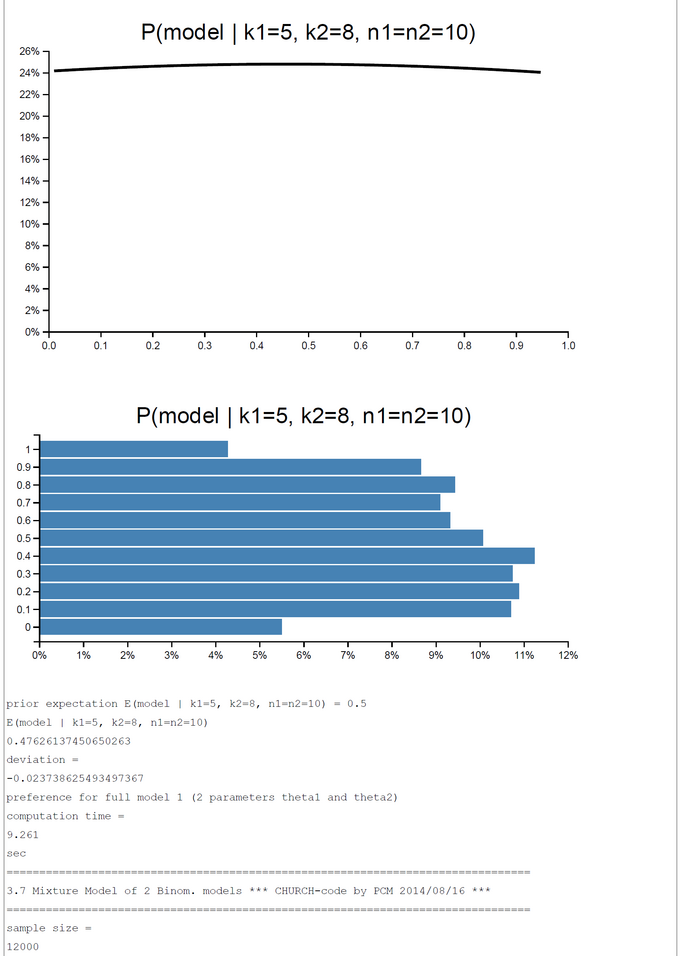
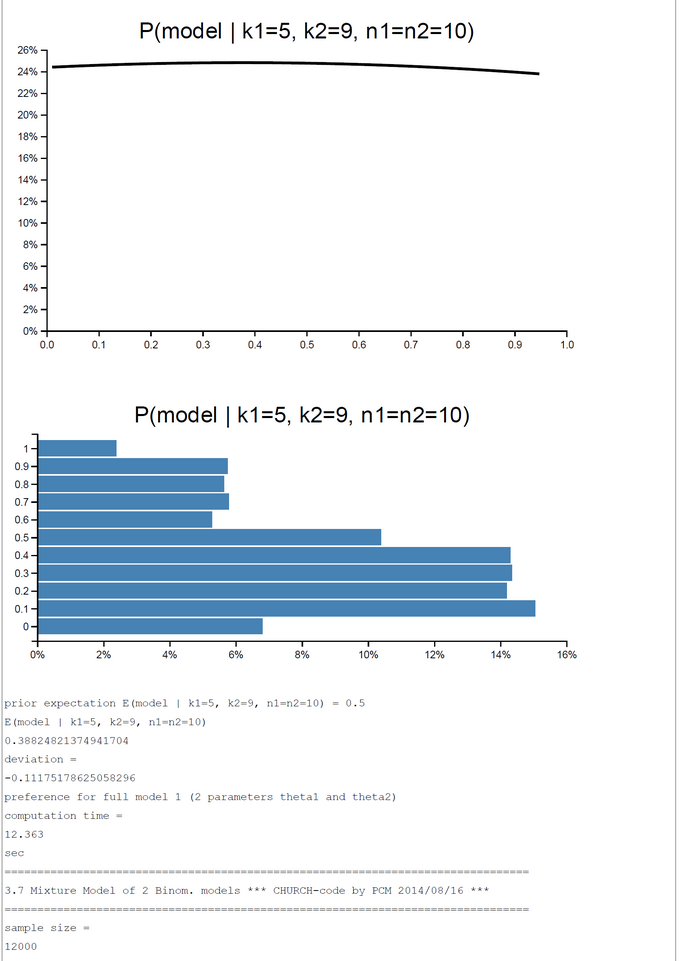
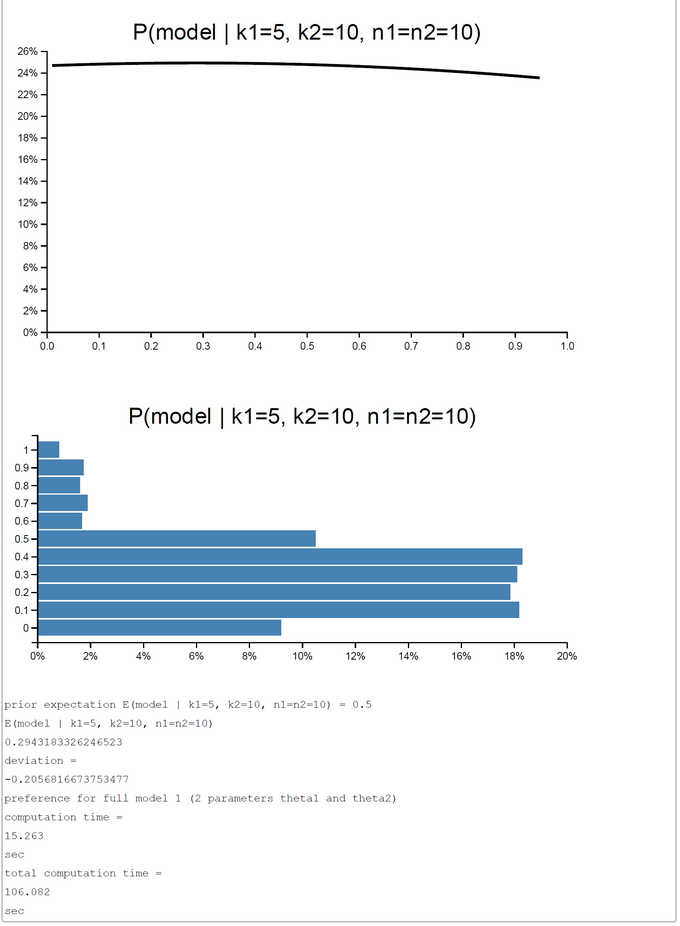
A pure and simple Bayesian analysis demonstrates the plausibility of each model by computing the posterior probability P(Model | k1, k2, n1, n2). By a numerical example with k1=5; k2=0, ... ,10; n1=n2=10 we can show that the posterior probability in favor of each model switches first between k2=2 and k2=3 and second between k2=7 and k2=8. For the range k2=3-7 the restricted model has a higher posterior probability and for k2=0-2, 8-10 the full model is more plausible.
The CHURCH-Code can be found here.