Periodic Thermodynamics
Periodic thermodynamics - a notion coined by Walter Kohn in 2001 - is a sidebranch of the physics of periodically driven quantum systems which is developing into a line of research of its own. It rests on the observation that a periodically driven quantum system in contact with a heat bath adopts a nonequilibrium steady state which is characterized by constant occupation probabilities of its Floquet states. Except for particular integrable model systems, the emerging Floquet-state occupation probability distribution (Fop distribution for short) not only is non-Boltzmannian, but also non-universal, in the sense that it depends on the details of the system-bath coupling.
In a joint work within our research group FOR 2692, published in Phys. Rev. Research 2, 023293 (2020), we have argued that a paramagnet, coupled to a heat bath, even can be transmuted into a diamagnet under strong periodic drving. This is a hard theoretical prediction which is now open to experimental verification.
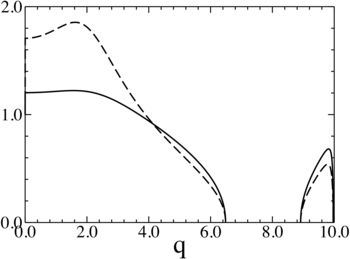
In a related case study reported in Phys. Rev. E 100, 012102 (2019) we have determined the Fop distribution for a parametrically driven harmonic oscillator for which it actually is of the Boltzmann type, but with a quasitemperature which differs from the true bath temperature. The above figure shows the scaled inverse quasitemperature (dashed) for such a Mathieu oscillator coupled to a heat bath with a Gaussian spectral density, together with its Floquet ground-state occupation probabilty (full line) vs. the scaled driving amplitude. For low driving strength the driven system is effectively colder than its environment, whereas its quasitemperature diverges at the stability borders.