Entdecker*innentage
Kontakt
Prof. Dr. Matthias Wollenhaupt
Carl von Ossietzky Universität Oldenburg
Fakultät V - Institut für Physik
Carl-Von-Ossietzky-Str. 9-11
D-26129 Oldenburg
Germany
Tel.: +49-441-798-3482
Raum: W2-1-101
matthias.wollenhaupt@uol.de
Entdecker*innentage
Ultraschnelle Superkontinuum-Pulsformung
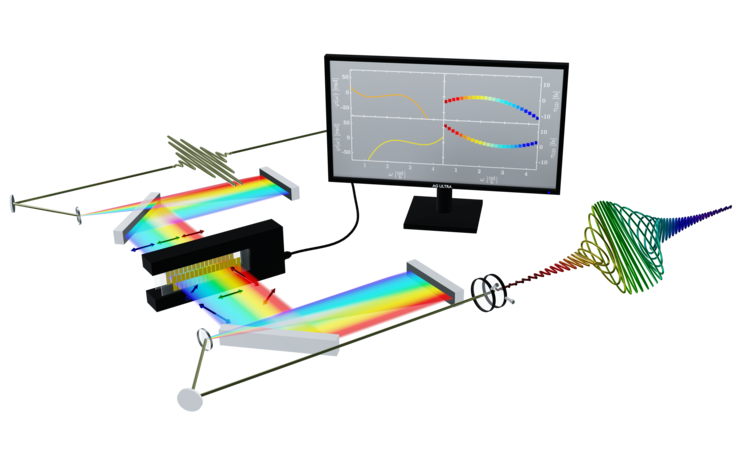
Ein ultrakurzer Laserpuls kann im Labor durch spektrale Phasenmodulationen beliebig geformt werden. Das Verfahren beruht hierbei auf transparenten Flüssigkristall-Displays (LCD von liquid crystal display), deren einzelne Pixel ansteuerbar und somit gezielt bezüglich des Brechungsindex manipulierbar sind.
Um einen Laserpuls mithilfe eines solchen Displays formen zu können, muss er zunächst in seine spektralen Bestandteile zerlegt werden. Dazu wird der Laserpuls (in der Abbildung oben links, weiß) auf ein Gitter geleitet, dessen Reflexionswinkel frequenzabhängig sind. Dadurch findet eine räumliche Zerlegung des Laserpulses in dessen Frequenzkomponenten statt, bzw. eine Fouriertransformation. Der aufgefächerte Strahl wird anschließend kollimiert und in die sogenannte Fourier-Ebene dirigiert in der sich das o.g. Display (schwarz Kasten) befindet. Durch Manipulation der Brechungsindizes der Flüssigkristall-Pixel (goldene Elemente) wird dann eine Phasenverschiebung der Frequenzkomponenten erreicht (daher der Begriff spektrale Phasenformung). Anschließend werden die Frequenzkomponenten durch einen gespiegelten Aufbau wieder vereint und ein geformter Puls entsteht.
Mit einem Pulsformer bestehend aus zwei Flüssigkristall-Displays deren optische Achsen im Winkel von +-45° zur Polarisation des einfallenden Laserpulses orientier sind, kann sowohl die spektrale Phase als auch die Polarisation des Laserpulses geformt werden. Mit dem Einsatz von Polarisatoren hinter den Displays kann die Polarisationsformung in eine Amplitudenmodulation übersetzt werden, Nachfolgend sind ein paar Beispiele für spektrale Femtosekunden Pulsformung visualisiert.
Pulsformung mit linearen spektralen Phasenfunktionen
In den hier dargestellten Beispielen ist die Variation des Parameters Φ der Phasenfunktion φ(ω)=Φ⋅ω gezeigt. Die Phasenfunktion ist auf der linken Seite des Monitors dargestellt. Zudem befinden sich zwei Polarisatoren hinter dem Pulsformer mit deren Hilfe zwei Spektralanteile aus dem Gesamtspektrum herausgefiltert werden. Mithilfe der Variation der Phasenfunktionen für die blaue und rote Komponente können die beiden Anteile zeitlich gegeneinander verzögert werden. Mathematisch wird dies über die sogenannte Gruppenverzögerung T(ω) (rechte Seite des Monitors) beschrieben. Die Gruppenverzögerung ist durch die Ableitung der spektralen Phase gegeben: T(ω)=dφ(ω)/dω = Φ.
Oberhalb ist die Pulsformung mit einer lineare Phasenfunktion der Form φ(ω)= Φω gezeigt. Wenn man nun diese Phasenfunktion um die Zentralwellenlänge ω0 des zu formenden Laserfeldes verschiebt, demnach die Phasenfunktion φ(ω)= Φ(ω-ω0) verwendet, wird der Puls nicht interferometrisch in der Zeit verschoben, wie es durch unterschiedlich lange Arme in in einem Interferometer der Fall wäre. Hier wird stattdessen nur die sogenannte Einhüllende verschoben.
Pulsformung mit quadratischen spektralen Phasenfunktionen
In dem oben abgebildeten Beispiel ist die Variation des Parameters Φ der Phasenfunktion φ(ω)=Φ⋅ω² visualisiert. Durch das Anlegen dieser Phase entsteht ein sogenannter gechirpter Puls, bei dem die Frequenzkomponenten ω linear gegeneinander verschoben sind. Dadurch treten sie nicht mehr gleichzeitig, sondern nacheinander auf, wobei - in Abhängigkeit des Vorzeichens von Φ - der Chirp (Zwitschern) aufwärts (von niedrigen zu hohen Frequenzen) oder abwärts (von hohen zu niedrigen Frequenzen) erfolgen kann. In der Abbildung sind jeweils Verläufe von Blau nach Rot und somit von hohen zu niedrigen Frequenzen gezeigt. Dies wird als Downchirp bezeichnet.
Der lineare Verlauf der Frequenz folgt mathematisch aus der Gruppenverzögerung T(ω). Diese ist durch die Ableitung der angelegten spektralen Phase gegeben: T(ω)=dφ(ω)/dω = Φ⋅ω. Diese lineare Verschiebung der Frequenzen ist in der obigen Abbildung direkt hinter dem Flüssigkristall-Display durch die farbigen Klötze dargestellt.
Weitere Beispiele für Pulsformung
Drehung des Laserpulses mit einer Halbwellenplatte
Hinter der Pulsformer ist eine Halbwellenplatte platzert. Diese kann die Polarisation von Laserfeldern drehen. Die Rotation von Laserpulsen ist ein wesentlicher Bestandteil der Photoelektroentomographie. Diese wird weiter unten auf dieser Seite beschrieben.
Velocity map imaging
Die sogenannte velocity map imaging Spektroskopie ist ein wichtiges Werkzeug in der experimentellen Atom- und Molekülphysik. Mit dieser Technik können mitunter Photoelektronen, die bei durch Multiphotonenionisation aus einem Atom oder Molekül herausgelöst werden, energie- und winkelaufgelöst detektiert werden. Hierzu werden die erzeugten Elektronen mittels elektrostatischen Feldern – erzeugt durch eine spezielle Anordnung von Elektroden – auf einen Detektor abgebildet bzw. projiziert. Im unterhalb zu sehenden Video, ist die Aufnahme einer solcher Projektion gezeigt.
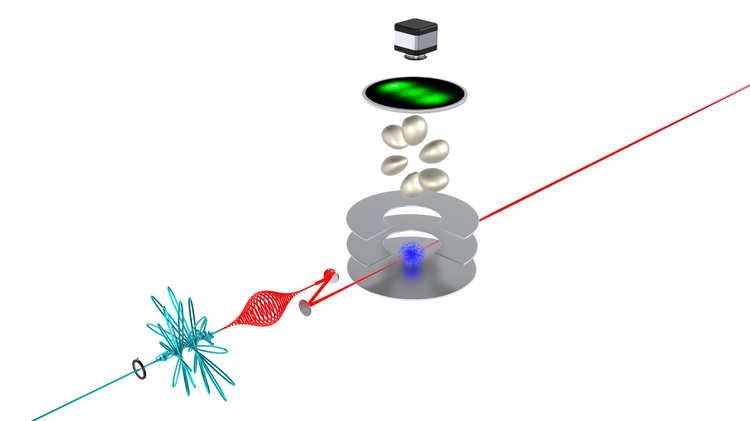
Photoelektronentomographie
Mit einer superachromatischen Halbwellenplatte wird die ionisierende polarisationsgeformte Laserpulssequenz rotiert. Dadurch wird ebenso das Photoelektronenwellenpaket gedreht. Für verschiedene Orientierungen der Elektronenverteilung wird deren Projektion auf einem Phosphorschrim detektiert und daraus letzlich das 3D Objekt rekonstruiert. In der Animation sind tatsächlich gemessene Projektionen und das daraus tomographisch rekonstruierte Photoelektronenwellenpaket in der Multiphotonenionisation von Kalium-Atomen gezeigt.