Ein ultrakurzer Laserpuls kann im Labor durch spektrale Phasenmodulationen beliebig geformt werden. Das Verfahren beruht hierbei auf transparenten Flüssigkristall-Displays (LCD von liquid crystal display), deren einzelne Pixel ansteuerbar und somit gezielt bezüglich des Brechungsindex manipulierbar sind.

Um einen Laserpuls mithilfe eines solchen Displays formen zu können, muss er zunächst in seine spektralen Bestandteile zerlegt werden. Dazu wird der Laserpuls (in der Abbildung oben links, grün) auf ein Gitter geleitet, dessen Reflexionswinkel frequenzabhängig sind. Dadurch findet eine räumliche Zerlegung des Laserpulses in dessen Frequenzkomponenten statt, bzw. eine Fouriertransformation. Der aufgefächerte Strahl wird anschließend kollimiert und in die sogenannte Fourier-Ebene dirigiert in der sich das o.g. Display (schwarz-grauer Kasten) befindet. Durch Manipulation der Brechungsindizes der Flüssigkristall-Pixel wird dann eine Phasenverschiebung der Frequenzkomponenten erreicht (daher der Begriff spektrale Phasenformung). Anschließend werden die Frequenzkomponenten durch einen gespiegelten Aufbau wieder vereint und ein geformter Puls entsteht.

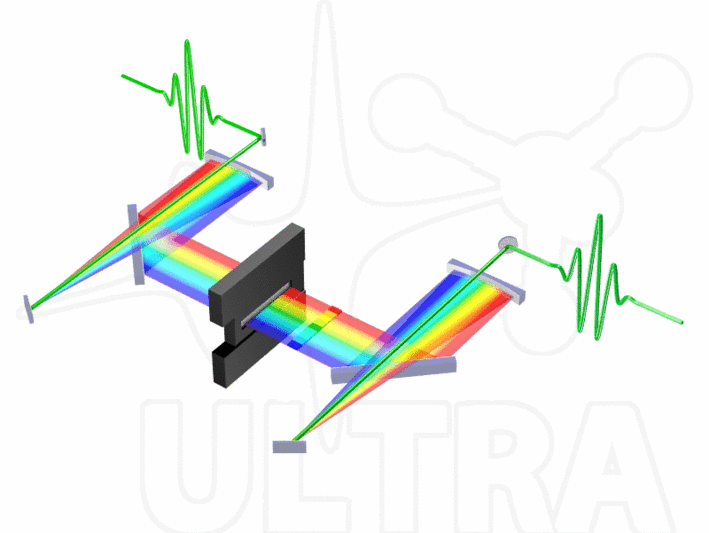
Pulsformung mit quadratischen spektralen Phasenfunktionen

In dem oben abgebildeten Beispiel ist die Variation des Parameters Φ der Phasenfunktion

φ(ω)=Φ/2⋅ω²

visualisiert. Durch das Anlegen dieser Phase entsteht ein sogenannter gechirpter Puls, bei dem die Frequenzkomponenten ω linear gegeneinander verschoben sind. Dadurch treten sie nicht mehr gleichzeitig, sondern nacheinander auf, wobei - in Abhängigkeit des Vorzeichens von Φ - der Chirp (Zwitschern) aufwärts (von niedrigen zu hohen Frequenzen) oder abwärts (von hohen zu niedrigen Frequenzen) erfolgen kann. In der Abbildung sind jeweils Verläufe von Blau nach Rot und somit von hohen zu niedrigen Frequenzen gezeigt. Dies wird als Downchirp bezeichnet.

Der lineare Verlauf der Frequenz folgt mathematisch aus der Gruppenverzögerung T(ω). Diese ist durch die Ableitung der angelegten spektralen Phase gegeben:

T(ω)=dφ(ω)/dω = Φ⋅ω

Diese lineare Verschiebung der Frequenzen ist in der obigen Abbildung direkt hinter dem Flüssigkristall-Display durch die farbigen Klötze dargestellt.

Pulsformung mit kubischen spektralen Phasenfunktionen

Wählt man für die oben eingeführte Phasenfunktion statt der quadratischen eine kubische Abhängigkeit von der Frequenz

φ(ω)=Φ/6⋅ω³

so verändert sich der geformte Ausgangspuls dramatisch. Die augenscheinlichste Veränderung besteht in der Farbe des Ausgangspulses, welche nun wieder identisch mit der des Eingangspulses ist (durchgängig grün). Dies lässt sich anhand der Gruppenverzögerung T(ω) leicht verstehen, welche sich wie oben erläutert aus der Ableitung der Phase ergibt:

T(ω)=Φ/2⋅ω²

Anders als die lineare Gruppenverzögerung des Chirps, ist die quadratische Gruppenverzögerung (farbige Klötzchen hinter dem LCD) der kubischen Phasenfunktion gerade. Das hat zur Folge, dass jeweils zwei symmetrisch um die Zentralfrequenz liegende Frequenzkomponenten gleich stark verzögert werden und per Schwebung wieder die Zentralfrequenz erzeugen. Eine zeitliche (räumliche) Abfolge verschiedener Frequenzkomponenten findet also nicht statt und der Ausgangspuls ist wie der Eingangspuls durchgängig grün.

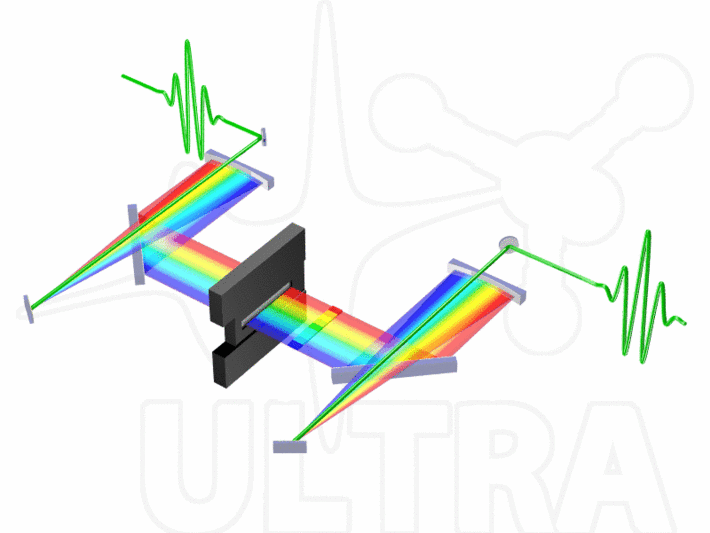
Auch das typische Airy-Funktionen-Profil des Ausgangspulses, welches einen ausgeprägten Hauptpuls und sukzessive kleiner werdende Satellitenpulse aufweist, kann aus der Form der Gruppenverzögerung abgeleitet werden. So wird der starke Hauptpuls durch den flachen Anteil am Scheitelpunkt der quadratischen Gruppenverzögerung erzeugt und die durch die o.g. Schwebung modulierten Satellitenpulse vermöge der symmetrisch ansteigenden Flanken von T(ω) gegen den Hauptpuls verschoben. Bei einem negativen Vorzeichen der kubischen Phase ist die Reihenfolge dieses Pulszuges genau umgekehrt.

Neben den polynomialen spektralen Phasenfunktionen gibt es noch eine Menge weiterer Möglichkeiten Laserpulse zu formen. Prinzipiell kann jede erdenkliche Funktion zur spektralen Phasenformung eingesetzt werden. Denkbar sind z.B. auch trigonometrische Funktionen wie der Sinus. Unten ist die Variation der Parameter A, T und Φ der Phasenfunktion

φ(ω)=A⋅sin((ω-0.5)⋅T+Φ)

gezeigt:

Der Ausgangspuls ist hier eine Multipulssequenz mit Einzelpulsen konstanter Instantanfrequenz. Die Amplitude des Sinus, also der Parameter A, steuert die Ausprägung der Einzelpulse, während die sogenannte Sinusfrequenz T deren zeitlichen Abstand festlegt. Eine Variation der Phase Φ beeinflusst die konstante Phase der Einzelpulse. Das hat zwar keinen Einfluss auf die Instantanfrequenz (welche die Ableitung der zeitlichen Phase ist), spielt jedoch bei phasensensitiven Prozessen wie der kohärenten Kontrolle eine bedeutende Rolle (u.A. Thema dieser Vorlesung).

Auch nicht-stetige Funktionen sind zur Pulsformung einsetzbar. Die Vorzeichen-Funktion sgn(x) z.B. ist durch

sgn(x)=-1, x<0 ∧ 1, x>0

definiert. Daraus lässt sich die sogenannte Theta-Step-Phasenfunktion

φ(ω)=θ/2⋅sgn(ω−δω)

ableiten, die beim Einsatz in der spektralen Phasenformung folgenden Einfluss auf den Laserpuls hat:

Der modulierte Puls ist hier eine Superposition des unmodulierten Eingangspulses und der Faltung des unmodulierten Pulses mit exp(i δω t)/ϖt.

Das ergibt in der Praxis eine an den Rändern mit 1/t abfallende Doppelpulssequenz. Die Lage der Lücke zwischen den beiden Pulsen wird dabei modulo 2ϖ durch die Sprunghöhe des Theta-Steps (also den Betrag von θ) und die Ausprägung der Lücke durch die Lage des Theta-Steps (also δω) festgelegt. Offensichtlich geht der modulierte Puls in den Eingangspuls über, wenn δω betragsgroße Werte annimmt bei denen sich der Theta-Step außerhalb des Spektrums befindet und das spektrale Feld im wesentlichen eine konstante Phase sieht.
Die Instantanfrequenz des modulierten Pulses ist in den mit 1/t abfallenden Flanken näherungsweise konstant und durch den Ort des Theta-Steps, also δω gegeben. Im Zeitbereich um die Lücke zwischen den beiden Teilpulsen macht die Instantanfrequenz einen Gauß-artigen Sprung, dessen Richtung (positiv oder negativ) vom Vorzeichen von δω abhängt.