Navigation
Baustein 8: Die Ionisierungsenergie
In Baustein 7 hast du das Energiestufen- und das Schalenmodell der Elektronenhülle kennengelernt. Einen wichtigen Beitrag zur Entwicklung dieser Modelle leisteten dabei Balmer und Rydberg, mit der von Ihnen entwickelten Formel. Mit dem Zusammenhang zwischen Wellenlänge und Energie des Lichtes, der von Einstein gefunden wurde konnte die Formel von Balmer und Rydberg interpretiert werden. Daraus konnten wir zunächst das Energiestufenmodell und dann das Schalenmodell der Elektronenhülle entwickeln.
In diesem Modell ist ein Wasserstoffatom aus einem Atomkern mit der Kernladung +1 und einem Elektron mit der Ladung -1 aufgebaut. Das Elektron befindet sich auf einer festgelegten Energiestufe, bzw. einer Schale mit festgelegtem Abstand zum Atomkern.
Mit der Rydberg-Formel
\(\frac{1}{\lambda}=R_\infty\cdot\left(\frac{1}{{n_1}^2}-\frac{1}{{n_2}^2}\right)\)
können wir die Wellenlänge des Lichtes bestimmen, die ein Elektron beim Übergang zwischen 2 Energiestufen aussendet.
Stellen wir uns nun vor, dass das Elektron des Wasserstoffatoms vom Grundzustand n1 = 1 in eine Energiestufe n2 übergehen soll, die quasi unendlich weit vom Atomkern entfernt ist. Da "unendlich" keine Zahl ist, die wir in die Formel einsetzen können, setzen wir bei der Berechnung für n2 einfach eine vergleichsweise sehr große Zahl ein, zum Beispiel 50. Dann erhalten wir für die Wellenlänge des Lichtes 91 nm.
Mit Hilfe von Einsteins Formel:
\(E= \frac{\left(h\cdot c\right)}{\lambda}\)
die den Zusammenhang zwischen Wellenlänge und Energie des Lichtes beschreibt, können wir auch berechnen wie viel Energie das Elektron aufnehmen muss, um auf diese Energiestufe zu gelangen. Wir erhalten eine Energie von 13,6 eV.
Wir haben angenommen, dass die Energiestufe 50 quasi unendlich weit vom Atomkern entfernt ist, aber wie können wir uns sicher sein, dass das so ist? Wenn wir die gleichen Berechnungen für die Energiestufe 100 durchführen, erhalten wir fast identische Werte für die Wellenlänge und die Energie. Sie unterscheiden sich zu den vorherigen erst in der 2. Nachkommastelle. Die Unterschiede sind also vernachlässigbar klein. Das Elektron kann maximal 13,6 eV Energie aufnehmen. Das ist die Energie, die benötigt wird, um das Elektron von der Anziehungskraft des Kerns positiv geladenen Kerns zu lösen.
Wir nennen diese Energie die Ionisierungsenergie.
Ionisierungsenergien der Elemente
Mit der Rydberg-Formel haben wir eine Möglichkeit die Ionisierungsenergie eines Wasserstoffatoms zu berechnen. Da, diese Formel aber nur das Wasserstoffatom beschreibt, können wir sie nicht auf andere Elemente anwenden, deren Atome einen komplexeren Aufbau als das Wasserstoffatom haben.
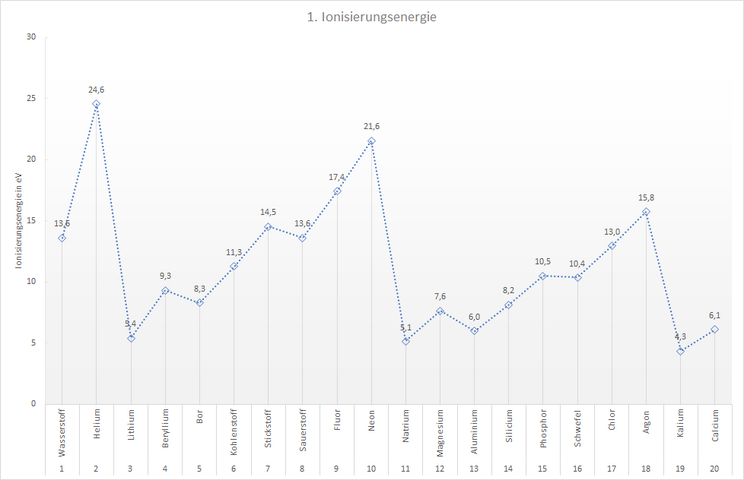
Die Ionisierungsenergie der Elemente kann aber mit Experimenten bestimmt werden. So können wir eine Tabelle aufstellen, die angibt, wie viel Energie mindestens notwendig ist, um einem Atom eines Elements genau ein Elektron zu entziehen. Diese 1. Ionisierungsenergie ist für die ersten 20 Elemente in der folgenden Tabelle dargestellt.
| Element | Ionisierungsenergie in eV |
|---|---|
| Wasserstoff | 13,6 |
| Helium | 24,6 |
| Lithium | 5,4 |
| Beryllium | 9,3 |
| Bor | 8,3 |
| Kohlenstoff | 11,3 |
| Stickstoff | 14,5 |
| Sauerstoff | 13,6 |
| Fluor | 17,4 |
| Neon | 21,6 |
| Natrium | 5,1 |
| Magnesium | 7,6 |
| Aluminium | 6,0 |
| Silicium | 8,2 |
| Phosphor | 10,5 |
| Schwefel | 10,4 |
| Chlor | 13,0 |
| Argon | 15,8 |
| Kalium | 4,3 |
| Calcium | 6,1 |
| ... |
Aufgabe
- Erstelle mit Hilfe der Tabelle ein Diagramm, welches den Verlauf der Ionisierungsenergie der ersten 20 Elemente zeigt.
- Formuliere anhand des Diagramms Regeln, die den groben Verlauf der Ionisierungsenergie beschreiben:
- Von oben nach unten (Innerhalb einer Hauptgruppe)...
- Von links nach rechts (Innerhalb einer Periode)...
Verlauf der Ionisierungsenergie im Periodensystem
Dein Diagramm sollte ungefähr so aussehen, wie das hier gezeigte Beispiel.
Du erkennst, dass...
- die Ionisierungsenergie innerhalb einer Hauptgruppe von oben nach unten abnimmt. Beispiel:
| Lithium | 5,4 eV |
| Natrium | 5,1 eV |
| Kalium | 4,3 eV |
- die Ionisierungsenergie innerhalb einer Periode von links nach rechts insgesamt ansteigt. Beispiel:
| Lithium | Beryllium | Bor | Kohlenstoff | Stickstoff | Sauerstoff | Fluor | Neon |
| 5,4 eV | 9,3 eV | 8,3 eV | 11,3 eV | 14,5 eV | 13,6 eV | 17,4 eV | 21,6 eV |
Aufgabe
- Begründe mit Hilfe des Schalenmodells der Elektronenhülle warum...
- ... die Ionisierungsenergie mit dem Beginn einer neuen Periode so stark abnimmt (Beispiel: von Neon zu Natrium).
- ... die Ionisierungsenergie innerhalb einer Hauptgruppe von oben nach unten abnimmt (Beispiel: von Lithium zu Kalium).
- ... die Ionisierungsenergie innerhalb einer Periode von links nach rechts insgesamt steigt (Beispiel: von Lithium zu Neon).
Besonders stabile Zustände
Sicher ist dir schon aufgefallen, dass die Ionisierungsenergie innerhalb einer Periode von links nach rechts nicht gleichmäßig ansteigt, sondern es sogar Elemente gibt, deren Ionisierungsenergie deutlich größer ist, als der Trend innerhalb der Periode. Ihre "Folgeelemente" haben eine geringere Ionisierungsenergie.
In der 2. Periode sind das die Elemente Beryllium und Stickstoff, in der 3. Periode Magnesium und Phosphor. Dieser Trend setzt sich in den folgenden Perioden fort: Die Elemente der 2. Hauptgruppe und die der 5. Hauptgruppe haben deutlich größere Ioniserungsenergien als anzunehmen wäre. Die Elektronen sind bei diesen Elementen also stärker an das Atom gebunden als bei ihren "Nachbarn".
Wenn sich auf der äußeren Schale 2 oder 5 Elektronen befinden, ist es schwieriger ein Elektron aus dem Atom zu entfernen als wenn die äußere Schale mit 3 oder 6 Elektronen besetzt wäre. Für unser Schalenmodell bedeutet das, dass es anscheinend besonders stabile Zustände für die Anordnung der Elektronen gibt. Eine Erklärung dafür kann uns das Schalenmodell nicht liefern.
Zurück zum vorherigen Baustein
Du hast es geschafft, klasse!
Du bist am Ende der Einheit angekommen. Du kannst jetzt noch die Übungsaufgaben bearbeiten.